The Birch and Swinnerton-Dyer Formula

``The subject of this lecture is rather a special one. I want to describe some computations undertaken by myself and Swinnerton-Dyer on EDSAC, by which we have calculated the zeta-functions of certain elliptic curves. As a result of these computations we have found an analogue for an elliptic curve of the Tamagawa number of an algebraic group; and conjectures have proliferated. [$\ldots$] I would like to stress that though the associated theory is both abstract and technically complicated, the objects about which I intend to talk are usually simply defined and often machine computable; experimentally we have detected certain relations between different invariants, but we have been unable to approach proofs of these relations, which must lie very deep.''
-Bryan Birch

Conjecture 2.17 (Birch and Swinnerton-Dyer)   Let $E$ be an elliptic curve over $\mathbb{Q}$ of rank $r$. Then $r = \ord _{s=1} L(E,s)$ and

$$\frac{L^{(r)}(E,1)}{r!} = \frac{\Omega_E \cdot \Reg (E) \cd... ...bb{Q}) \cdot \prod_{p} c_p }{\char93 E(\mathbb{Q})_{\tor }^2}.$$ (2.3.1)

Let

$$y^2 + \underline{a}_1 xy + \underline{a}_3 y = x^3 +\underline{a}_2 x^2 + \underline{a}_4 x + \underline{a}_6$$ (2.3.2)

be a minimal Weierstrass equation for $E$.

Recall from Section 1.5.2 that the real period $\Omega_E$ is the integral

$$\Omega_E = \int_{E(\mathbb{R})} \frac{dx}{2y + \underline{a}_1 x + \underline{a}_3}.$$

See [Cre97, §3.7] for an explanation about how to use the Gauss arithmetic-geometry mean to efficiently compute $\Omega_E$.

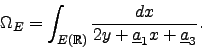
To define the regulator $\Reg (E)$ let $P_1,\ldots, P_n$ be a basis for $E(\mathbb{Q})$ modulo torsion and recall the Néron-Tate canonical height pairing $\langle , \rangle$ from Section 1.2. The real number $\Reg (E)$ is the absolute value of the determinant of the $n\times n$ matrix whose $(i,j)$ entry is $\langle P_i, P_j \rangle$. See [Cre97, §3.4] for a discussion of how to compute $\Reg (E)$.

We defined the group ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ in Section 2.2.4. In general it is not known to be finite, which led to Tate's famous assertion that the above conjecture ``relates the value of a function at a point at which it is not known to be defined to the order of a group that is not known to be finite.'' The paper [GJP⁺05] discusses methods for computing $\char93 {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ in practice, though no general algorithm for computing $\char93 {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ is known. In fact, in general even if we assume truth of the BSD rank conjecture (Conjecture 1.1) and assume that ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ is finite, there is still no known way to compute $\char93 {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$, i.e., there is no analogue of Proposition 1.3. Given finiteness of ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ we can compute the $p$-part ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})(p)$ of ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ for any prime $p$, but we don't know when to stop considering new primes $p$. (Note that when $r_{E,{\rm an}}\leq 1$, Kolyvagin's work provides an explicit upper bound on $\char93 {\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$, so in that case ${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E/\mathbb{Q})$ is computable.)

The Tamagawa numbers $c_p$ are $1$ for all primes $p\nmid \Delta_E$, where $\Delta_E$ is the discriminant of (2.3.2). When $p\mid \Delta_E$, the number $c_p$ is a more refined measure of the structure of the $E$ locally at $p$. If $p$ is a prime of additive reduction (see Section 1.3), then one can prove that $c_p \leq 4$. The other alternatives are that $p$ is a prime of split or nonsplit multiplicative reduction. If $p$ is a nonsplit prime, then

$$c_p = \begin{cases}1 & \text{ if $\ord _p(\Delta)$ is odd} \\ 2 & \text{ otherwise} \end{cases}$$

If $p$ is a prime of split multiplicative reduction then

$$c_p = \ord _p(\Delta)$$

can be arbitrarily large. The above discussion completely determines $c_p$ except when $p$ is an additive prime - see [Cre97, §3.2] for a discussion of how to compute $c_p$ in general.

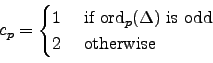
For those that are very familiar with elliptic curves over local fields,

$$c_p = [E(\mathbb{Q}_p) : E^0(\mathbb{Q}_p)],$$

where $E^0(\mathbb{Q}_p)$ is the subgroup of $E(\mathbb{Q}_p)$ of points that have nonsingular reduction modulo $p$.

For those with more geometric background, we offer the following conceptual definition of $c_p$. Let $\mathcal{E}$ be the Néron model of $E$. This is the unique, up to unique isomorphism, smooth commutative (but not proper!) group scheme over $\mathbb{Z}$ that has generic fiber $E$ and satisfies the Néron mapping property:

for any smooth group scheme $X$ over $\mathbb{Z}$ the natural map

$$\Hom (X, \mathcal{E}) \to \Hom (X_\mathbb{Q}, E)$$

is an isomorphism.

In particular, note that $\mathcal{E}(\mathbb{Z}) \cong E(\mathbb{Q})$. For each prime $p$, the reduction $\mathcal{E}_{\mathbb{F}_p}$ of the Néron model modulo $p$ is a smooth commutative group scheme over $\mathbb{F}_p$ (smoothness is a property of morphisms that is closed under base extension). Let $\mathcal{E}_{\mathbb{F}_p}^0$ be the identity component of the group scheme $\mathcal{E}_{\mathbb{F}_p}$, i.e., the connected component of $\mathcal{E}_{\mathbb{F}_p}^0$ that contains the $0$ section. The component group of $E$ at $p$ is the quotient group scheme

$$\Phi_{E,p} = \mathcal{E}_{\mathbb{F}_p} / \mathcal{E}_{\mathbb{F}_p}^0,$$

which is a finite étale group scheme over $\mathbb{F}_p$. Finally

$$c_p = \char93 \Phi_{E,p}(\mathbb{F}_p).$$