Next: Some Conjectures and Theorems Up: The Shafarevich-Tate Group Previous: The Selmer Group Contents Index
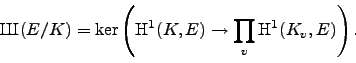
For any positive integer ![]() ,
we may thus add in a row to (2.2.2):
,
we may thus add in a row to (2.2.2):
![\begin{displaymath}
\xymatrix @=1.2em{
0 \ar[r]& {E(K)/n E(K)} \ar[r]\ar[d]& {\...
... \H^1(K_v,E[n])}
\ar[r]& {\prod_v H^1(K_v,E)[n]} \ar[r]& 0.
}
\end{displaymath}](img378.png)
The ![]() -descent sequence for
-descent sequence for ![]() is the short exact sequence
is the short exact sequence
![\begin{proof}
% latex2html id marker 4433
[Sketch of Proof]
Let $K(E[n])$ denot...
...ly that there are only
finitely many such extensions of $K[n]$.
\par
\end{proof}](img383.png)
William 2007-05-25