The Complex 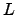 -series
-series 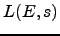
In Section 1.1 we defined a function
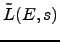 ,
which encoded information about
,
which encoded information about
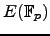 for all but finitely
many primes
for all but finitely
many primes 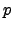 . In this section we define the function
. In this section we define the function 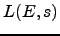 ,
which includes information about all primes, and the function
,
which includes information about all primes, and the function
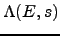 that also includes information ``at infinity''.
that also includes information ``at infinity''.
Let  be an elliptic curve over
be an elliptic curve over 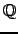 defined by a
minimal Weierstrass equation
defined by a
minimal Weierstrass equation
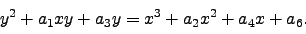 |
(1.3.1) |
A minimal Weierstrass equation in one for which the 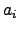 are all integers and the discriminant
are all integers and the discriminant
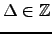 is minimal
amongs all discriminants of Weierstrass equations for
is minimal
amongs all discriminants of Weierstrass equations for  (again, see [Sil92] for the definition of the
discriminant of a Weierstrass equation, and also for an
explicit description of the allowed transformations of
a Weierstrass equation).
(again, see [Sil92] for the definition of the
discriminant of a Weierstrass equation, and also for an
explicit description of the allowed transformations of
a Weierstrass equation).
For each prime number 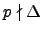 , the equation
(1.3.1) reduces modulo
, the equation
(1.3.1) reduces modulo 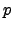 to define an elliptic
to define an elliptic
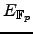 over the finite field
over the finite field 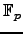 . Let
. Let
For each prime 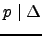 , we use the following
recipe to define
, we use the following
recipe to define 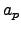 . If the singular curve
. If the singular curve
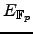 has a cuspidal singularity, e.g., is
has a cuspidal singularity, e.g., is
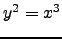 , then let
, then let 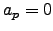 . If it has a a nodal
singularity, e.g., like
. If it has a a nodal
singularity, e.g., like 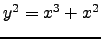 , let
, let 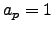 if the slope of the tangent line at the singular
point is in
if the slope of the tangent line at the singular
point is in 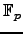 and let
and let 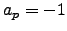 if the slope is
not in
if the slope is
not in 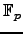 . Summarizing:
. Summarizing:
Even in the cases when 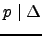 , we still have
, we still have
When  has additive reduction, the nonsingular points
form a group isomorphic to
has additive reduction, the nonsingular points
form a group isomorphic to
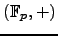 , and there is
one singular point, hence
, and there is
one singular point, hence 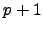 points,
so
points,
so
When  has split multiplicative reduction, there is 1 singular
point plus the number of elements of a group isomorphic to
has split multiplicative reduction, there is 1 singular
point plus the number of elements of a group isomorphic to
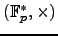 ,
so
,
so 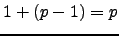 points, and
points, and
When  has non-split multiplicative
reduction, there is
has non-split multiplicative
reduction, there is 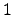 singular point plus the number
of elements of a group isomorphic
singular point plus the number
of elements of a group isomorphic
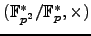 ,
i.e.,
,
i.e., 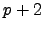 points, and
points, and
The definition of the full 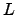 -function of
-function of  is then
is then
If in addition we add in a few more analytic factors to the 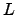 -function
we obtain a function
-function
we obtain a function 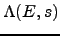 that satisfies a remarkably simple
functional equation.
Let
that satisfies a remarkably simple
functional equation.
Let
be the 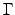 -function (e.g.,
-function (e.g.,
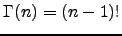 ),
which defines a meromorphic function on
),
which defines a meromorphic function on 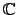 , with poles
at the non-positive integers.
, with poles
at the non-positive integers.
Theorem 1.6 (Hecke, Wiles et al.)
There is a unique positive integer 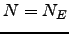 and sign
and sign
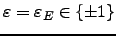 such that the function
extends to a complex analytic function on all
such that the function
extends to a complex analytic function on all 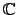 that
satisfies the functional equation
that
satisfies the functional equation
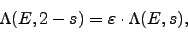 |
(1.3.2) |
for all
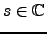 .
.
The integer 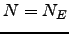 is called the conductor of
is called the conductor of
 and
and
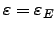 is called the sign in the functional
equation for
is called the sign in the functional
equation for  or the root number of
or the root number of  .
One can prove that the primes that divide
.
One can prove that the primes that divide 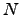 are the same
as the primes that divide
are the same
as the primes that divide 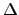 . Moreover, for
. Moreover, for 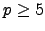 ,
we have that
,
we have that
There is a geometric algorithm called Tate's algorithm that
computes 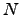 in all cases and
in all cases and 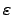 .
.
Example 1.7
Consider the elliptic curve

defined by
The above Weierstrass equation is minimal and
has discriminant
sage: e = EllipticCurve('1925d'); e
Elliptic Curve defined by y^2 + y = x^3 + 50*x + 31 over Rational Field
sage: e.is_minimal()
True
sage: factor(e.discriminant())
-1 * 5^6 * 7^2 * 11
At 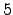 the curve has additive reduction so
the curve has additive reduction so 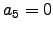 .
At
.
At 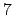 the curve has split multiplicative reduction
so
the curve has split multiplicative reduction
so 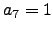 . At
. At 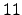 the curve has nonsplit multiplicative
reduction, so
the curve has nonsplit multiplicative
reduction, so 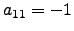 . Counting points for
. Counting points for 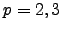 ,
we find that
,
we find that
sage: [e.ap(p) for p in primes(14)]
[0, 3, 0, 1, -1, 4]

Conjecture 1.9 (The Parity Conjecture)
Let  be an elliptic curve over
be an elliptic curve over 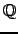 , let
, let
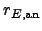 be the
analytic rank and
be the
analytic rank and 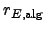 be the algebraic rank. Then
be the algebraic rank. Then
Jan Nekovar has done a huge amount of work toward
Conjecture 1.9; in particular, he proves it under the
(as yet unproved) hypothesis that
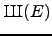 is finite (see
Section 2.2 below).
is finite (see
Section 2.2 below).
William
2007-05-25
![]() be an elliptic curve over
be an elliptic curve over ![]() defined by a
minimal Weierstrass equation
defined by a
minimal Weierstrass equation
![]() , the equation
(1.3.1) reduces modulo
, the equation
(1.3.1) reduces modulo ![]() to define an elliptic
to define an elliptic
![]() over the finite field
over the finite field ![]() . Let
. Let

![]() , we still have
, we still have
![]() -function of
-function of ![]() is then
is then
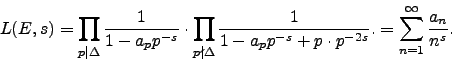
![]() -function
we obtain a function
-function
we obtain a function ![]() that satisfies a remarkably simple
functional equation.
Let
that satisfies a remarkably simple
functional equation.
Let
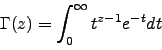
![]() is called the conductor of
is called the conductor of
![]() and
and
![]() is called the sign in the functional
equation for
is called the sign in the functional
equation for ![]() or the root number of
or the root number of ![]() .
One can prove that the primes that divide
.
One can prove that the primes that divide ![]() are the same
as the primes that divide
are the same
as the primes that divide ![]() . Moreover, for
. Moreover, for ![]() ,
we have that
,
we have that

![]() the curve has additive reduction so
the curve has additive reduction so ![]() .
At
.
At ![]() the curve has split multiplicative reduction
so
the curve has split multiplicative reduction
so ![]() . At
. At ![]() the curve has nonsplit multiplicative
reduction, so
the curve has nonsplit multiplicative
reduction, so ![]() . Counting points for
. Counting points for ![]() ,
we find that
,
we find that
