Computing $L(E,s)$

In this section we briefly describe one way to evaluate $L(E,s)$, for $s$ real. See [Dok04] for a more sophisticated analysis of computing $L(E,s)$ and its Taylor expansion for any complex number $s$.

Theorem 1.10 (Lavrik)   We have the following rapidly-converging series expression for $L(E,s)$, for any complex number $s$:

$$L(E,s) = N^{-s/2}\cdot (2\pi)^s\cdot \Gamma(s)^{-1}\cdot \su... ...\infty} a_n \cdot \left(F_n(s-1) - \varepsilon F_n(1-s)\right)$$

where

$$F_n(t) = \Gamma\left(t+1, \frac{2\pi n}{\sqrt{N}}\right) \cdot \left(\frac{\sqrt{N}}{2\pi n}\right)^{t+1},$$

and

$$\Gamma(z,\alpha) = \int_{\alpha}^{\infty} t^{z-1} e^{-t}dt$$

is the incomplete $\Gamma$-function.

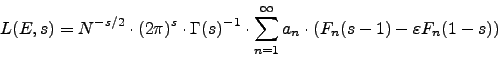
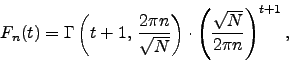
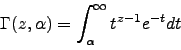
Theorem 1.10 above is a special case of a more general theorem that gives rapidly converging series that allow computation of any Dirichlet series $\sum a_n n^s$ that meromorphically continues to the whole complex plane and satisfies an appropriate functional equation. For more details, see [Coh00, §10.3], especially Exercise 24 on page 521 of [Coh00].