Next: The -adic -series Up: Computing Previous: Computing Contents Index
In this section, we describe a slightly different method, which only uses Theorem 1.10 and the definition of the derivative.
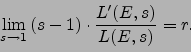
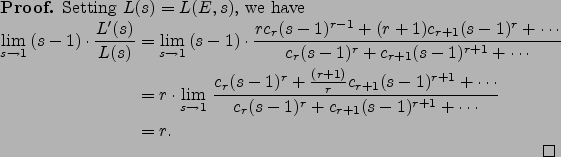
Thus the rank ![]() is
the limit as
is
the limit as
![]() of a certain (smooth) function. We know this
limit is an integer. But, for example, for the rank
of a certain (smooth) function. We know this
limit is an integer. But, for example, for the rank ![]() curve
curve
Using the definition of derivative, we approximate
![]() as follows. For
as follows. For ![]() small, we have
small, we have
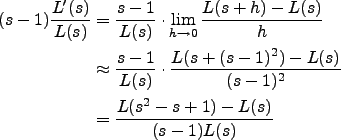
In fact, we have
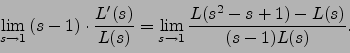
We can use this formula in SAGE to
``approximate'' ![]() . First we start
with a curve of rank
. First we start
with a curve of rank ![]() .
.
sage: e = EllipticCurve('389a'); e.rank()
2
sage: L = e.Lseries_dokchitser()
sage: def r(e,s): L1=L(s); L2=L(s^2-s+1); return (L2-L1)/((s-1)*L1)
sage: r(e,1.01)
2.00413534247395
sage: r(e,1.001)
2.00043133754756
sage: r(e,1.00001)
2.00000433133371
Next consider the curve
![]() of rank
of rank ![]() :
:
sage: e = EllipticCurve([1, -1, 0, -79, 289])
sage: e.rank()
4
sage: L = e.Lseries_dokchitser(100)
sage: def r(e,s): L1=L(s); L2=L(s^2-s+1); return (L2-L1)/((s-1)*L1)
sage: R = RealField(100)
sage: r(e,R('1.01'))
4.0212949184444018810727106489
sage: r(e,R('1.001'))
4.0022223745190806421850637523
sage: r(e,R('1.00001'))
4.0000223250026401574120263050
sage: r(e,R('1.000001'))
4.0000022325922257758141597819
It certainly looks like
![]() . We know that
. We know that
![]() , and if only there were a good way to bound
the error we could conclude that the limit is
, and if only there were a good way to bound
the error we could conclude that the limit is ![]() . But this has
stumped people for years, and probably it is nearly impossible without
a deep result that somehow interprets
. But this has
stumped people for years, and probably it is nearly impossible without
a deep result that somehow interprets ![]() in a completely
different way.
in a completely
different way.
William 2007-05-25