Question 1.13
Let

vary over all elliptic curve over
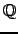
and
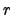
over all rational numbers. Is the set
of denominators of the rational numbers
![$[r]_E$](img169.png)
bounded? Thoughts: For a given curve

, the
denominators are bounded by the order of the image
in
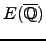
of the cuspidal subgroup of
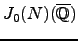
. It is likely one can show that
if a prime
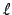
divides the order of the image
of this subgroup, then

admits a rational
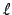
-isogeny.
Mazur's theorem would then prove that the set of such
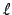
is bounded, which would imply a ``yes'' answer
to this question. Also, for any particular curve

,
one can compute the cuspidal subgroup precisely, and
hence bound the denominators of
![$[r]_E$](img169.png)
.
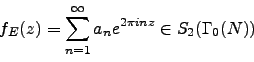
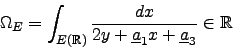
![]() is the map
is the map
![]() given by sending
given by sending
![]() to
to
![\begin{displaymath}[r]= [r]_E=
\frac{2 \pi i }{\Omega_E}
\left( \int_r^{i\infty} f_E(z) dz + \int_{-r}^{i\infty} f_E(z) dz
\right).
\end{displaymath}](img168.png)
![]() be the
be the ![]() th Fourier coefficient of
th Fourier coefficient of ![]() and note
that the polynomial
and note
that the polynomial
![\begin{displaymath}
\mu_E(a+p^n \mathbb{Z}_p) =
\frac{1}{\alpha^n} \left[\frac{...
...right] -\frac{1}{\alpha^{n+1}} \left[\frac{a}{p^{n-1}}\right].
\end{displaymath}](img177.png)