Hensel's lemma and the Teichmuller lift
The following standard lemma is proved by Newton iteration.
For example, consider the polynomial
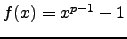 . By
Fermat's little theorem, it has
. By
Fermat's little theorem, it has 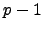 distinct roots in
distinct roots in
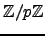 ,
so by Lemma 1.12 there are
,
so by Lemma 1.12 there are 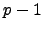 roots of
roots of 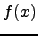 in
in 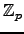 , i.e., all the
, i.e., all the 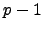 st roots of unity are elements of
st roots of unity are elements of
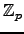 . The Teichmuller lift is the map that sends
any
. The Teichmuller lift is the map that sends
any
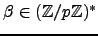 to the unique
to the unique 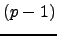 st root of unity
in
st root of unity
in
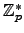 that reduces to it.
that reduces to it.
The Teichmuller character is the homomorphism
obtained by first reducing modulo 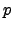 , then sending an element
to its Teichmuller lift.
The
, then sending an element
to its Teichmuller lift.
The 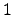 -unit projection character is the homomorphism
-unit projection character is the homomorphism
given by
William
2007-05-25