


Next: Visible Elements of
Up: Construction of Visible Elements
Previous: Tamagawa Numbers
Smoothness and Surjectivity
In this section, we recall some well-known lemmas that we will use in
Section 3.4 to produce unramified cohomology classes.
The authors are grateful to B. Conrad for explaining the proofs of
these lemmas.
Lemma 3.3
If
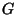
is a finite-type smooth commutative group scheme over a
strictly henselian local ring
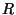
and the fibers of
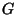
over
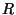
are
(geometrically) connected, then the multiplication map
is
surjective when
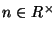
.
Proof.
Pick an element
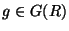
and form the cartesian diagram
We want to prove that
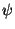
has a section.
Since
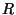
is strictly henselian, by [
Gro67, 18.8.1]
it suffices to show that
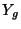
is étale over
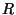
with non-empty
closed fiber, or more generally that
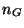
is étale and
surjective.
By Lemma 2(b) of [BLR90, §7.3],
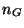 is étale.
The image of the étale
is étale.
The image of the étale 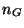 must be an open subgroup scheme, and on
fibers over
must be an open subgroup scheme, and on
fibers over 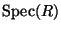 we get surjectivity since an open subgroup
scheme of a smooth connected (hence irreducible)
group scheme over a field must fill up the whole
space [Gro70, VI
we get surjectivity since an open subgroup
scheme of a smooth connected (hence irreducible)
group scheme over a field must fill up the whole
space [Gro70, VI
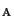 , 0.5].
, 0.5].

Lemma 3.4
Let
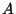
be an abelian variety over the fraction field
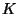
of a
strictly henselian
dvr (e.g.,
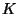
could be the maximal unramified extension
a local field).
Let
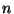
be an integer not divisible by
the residue characteristic of
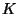
.
Suppose that
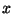
is a point of
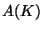
whose reduction lands in the
identity component of the closed fiber of the Néron model
of
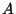
. Then there exists
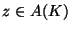
such that
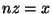
.
Proof.
Let
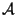
denote the Néron model of
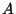
over the
valuation ring
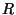
of
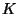
, and let
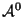
denote
the ``identity component'' (i.e., the open subgroup scheme
obtained by removing the non-identity components of
the closed fiber of
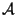
). The hypothesis on the reduction of
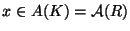
says exactly that
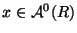
.
Since connected schemes
over a field are geometrically connected
when there is a rational point [
Gro65, Prop. 4.5.13],
the fibers of
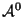
over
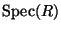
are
geometrically connected.
The lemma now follows from Lemma
3.3 with
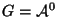
.

Remark 3.5
M. Baker noted that this argument can also be
formulated in terms of formal groups when
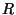
is the strict henselization of a
complete dvr.
Lemma 3.6
Let
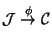
be a smooth surjective morphism of
schemes over a strictly Henselian local ring
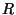
. Then the
induced map
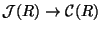
is surjective.
Proof.
The argument is similar to that of the proof of Lemma
3.3.
Pick an element
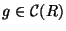
and form the cartesian diagram
We want to prove that
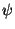
has a section.
Since
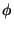
is smooth,
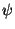
is also smooth.
By [
Gro67, 18.5.17], to show that
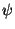
has a section,
we just need to show that the closed fiber of
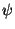
has
a section (i.e., a rational point). But this closed fiber
is smooth and non-empty (since
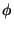
is surjective); also
its base field is separably closed since
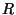
is strictly Henselian.
Hence by
[
BLR90, Cor. 2.2.13], the closed fiber has
an
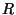
-rational point.




Next: Visible Elements of
Up: Construction of Visible Elements
Previous: Tamagawa Numbers
William A Stein
2002-02-27
![$\displaystyle \xymatrix @=3pc{
Y_g \ar[rr]^{\psi}\ar[d] && {\Spec(R)}\ar[d]^{g}\\
G\ar[rr]^{n_G} && G}$](img120.png)
![]() is étale.
The image of the étale
is étale.
The image of the étale ![]() must be an open subgroup scheme, and on
fibers over
must be an open subgroup scheme, and on
fibers over ![]() we get surjectivity since an open subgroup
scheme of a smooth connected (hence irreducible)
group scheme over a field must fill up the whole
space [Gro70, VI
we get surjectivity since an open subgroup
scheme of a smooth connected (hence irreducible)
group scheme over a field must fill up the whole
space [Gro70, VI
![]() , 0.5].
, 0.5].
![]()
![$\displaystyle \xymatrix @=3pc{
Y_g \ar[rr]^{\psi}\ar[d] && {\Spec(R)}\ar[d]^{g}\\
\mathcal{J}\ar[rr]^{\phi} && \mathcal{C}}$](img135.png)