


Next: Smoothness and Surjectivity
Up: Construction of Visible Elements
Previous: Construction of Visible Elements
Tamagawa Numbers
Let 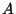 be an abelian variety over a local
field
be an abelian variety over a local
field 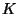 with residue class field
with residue class field 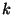 ,
and let
,
and let
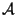 be the Néron model of
be the Néron model of 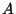 over the ring
of integers of
over the ring
of integers of 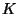 . The closed fiber
. The closed fiber
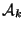 of
of
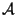 need not be
connected.
Let
need not be
connected.
Let
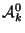 denote the geometric component of
denote the geometric component of
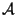 that contains the identity. The group
that contains the identity. The group
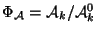 of connected components is a finite group scheme over
of connected components is a finite group scheme over 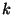 .
This group scheme is called the component group of
.
This group scheme is called the component group of
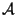 ,
and the Tamagawa number of
,
and the Tamagawa number of 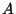 is
is
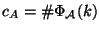 .
.
Now suppose that 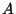 is an abelian variety over a global field
is an abelian variety over a global field 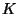 .
For every place
.
For every place 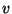 of
of 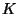 , the Tamagawa number of
, the Tamagawa number of 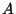 at
at 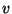 ,
denoted
,
denoted 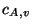 or just
or just 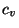 , is the Tamagawa number of
, is the Tamagawa number of 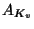 ,
where
,
where 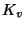 is the completion of
is the completion of 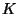 at
at 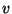 .
.
William A Stein
2002-02-27
![]() is an abelian variety over a global field
is an abelian variety over a global field ![]() .
For every place
.
For every place ![]() of
of ![]() , the Tamagawa number of
, the Tamagawa number of ![]() at
at ![]() ,
denoted
,
denoted ![]() or just
or just ![]() , is the Tamagawa number of
, is the Tamagawa number of ![]() ,
where
,
where ![]() is the completion of
is the completion of ![]() at
at ![]() .
.