Bibliography

AS02

A. Agashe and W.A. Stein, Visible Evidence for the Birch and Swinnerton-Dyer Conjecture for Rank 0 Modular Abelian Varieties, Preprint.

BCP97

W. Bosma, J. Cannon, and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), no. 3-4, 235-265, Computational algebra and number theory (London, 1993).

BLR90

S. Bosch, W. Lütkebohmert, and M. Raynaud, Néron models, Springer-Verlag, Berlin, 1990.

Cas63

J.W.S. Cassels, Arithmetic on curves of genus 1. V. Two counterexamples, J. London Math. Soc. 38 (1963), 244-248.

CM00

J.E. Cremona and B. Mazur, Visualizing elements in the Shafarevich-Tate group, Experiment. Math. 9 (2000), no. 1, 13-28.

Cre

J.E. Cremona, Elliptic curves of conductor $\leq 12000$,
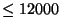http://www.maths.nott.ac.uk/personal/jec/ftp/data/.

Cre97

J.E. Cremona, Algorithms for modular elliptic curves, second ed., Cambridge University Press, Cambridge, 1997.

Edi92

B. Edixhoven, The weight in Serre's conjectures on modular forms, Invent. Math. 109 (1992), no. 3, 563-594.

Gro65

A. Grothendieck, Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II, Inst. Hautes Études Sci. Publ. Math. (1965), no. 24, 231.

Gro66

A. Grothendieck, Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III, Inst. Hautes Études Sci. Publ. Math. (1966), no. 28, 255.

Gro67

A. Grothendieck, Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Inst. Hautes Études Sci. Publ. Math. (1967), no. 32, 361.

Gro70

A. Grothendieck, Schémas en groupes. I: Propriétés générales des schémas en groupes, Springer-Verlag, Berlin, 1970.

Kle01

T. Klenke, Modular Varieties and Visibility, Ph.D. thesis, Harvard University (2001).

LT58

S. Lang and J. Tate, Principal homogeneous spaces over abelian varieties, Amer. J. Math. 80 (1958), 659-684.

Maz99

B. Mazur, Visualizing elements of order three in the Shafarevich-Tate group, Asian J. Math. 3 (1999), no. 1, 221-232.

Mil86

J.S. Milne, Arithmetic duality theorems, Academic Press Inc., Boston, Mass., 1986.

O'N01

C. O'Neil, The period-index obstruction for elliptic curves, to appear in Journal of Number Theory.

Rib90

K.A. Ribet, Raising the levels of modular representations, Séminaire de Théorie des Nombres, Paris 1987-88, Birkhäuser Boston, Boston, MA, 1990, pp. 259-271.

Ser79

J-P. Serre, Local fields, Springer-Verlag, New York, 1979, Translated from the French by Marvin Jay Greenberg.

Ste00

W.A. Stein, Explicit approaches to modular abelian varieties, Ph.D. thesis, University of California, Berkeley (2000).

Stu87

J. Sturm, On the congruence of modular forms, Number theory (New York, 1984-1985), Springer, Berlin, 1987, pp. 275-280.