- When
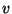 is real archimedian, we use that
is real archimedian, we use that
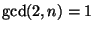 .
(We know that for any
.
(We know that for any 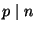 we have
we have
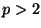 because
because
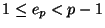 , by assumption.)
, by assumption.)
- When
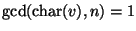 , we use the result of
Section 3.2 and a relationship between unramified
cohomology and the cohomology of a component group.
, we use the result of
Section 3.2 and a relationship between unramified
cohomology and the cohomology of a component group.
- When
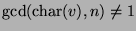 , for each prime
, for each prime 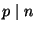 ,
the reduction of
,
the reduction of 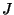 is abelian
and by hypothesis
is abelian
and by hypothesis 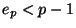 , so we can apply an exactness theorem
from [BLR90].
, so we can apply an exactness theorem
from [BLR90].
We now deduce that the image of
![]() in
in ![]() lies in
lies in
![]() . Fix an element
. Fix an element ![]() . To show that
. To show that
![]() , it suffices to show that
, it suffices to show that
![]() for all
places
for all
places ![]() of
of ![]() .
.
Case 1.
![]() real archimedian:
At a real archimedian place
real archimedian:
At a real archimedian place ![]() ,
the restriction
,
the restriction
![]() is killed by
is killed by ![]() and the odd
and the odd ![]() ,
hence
,
hence
![]() .
.
Case 2.
![]() :
Suppose that
:
Suppose that
![]() .
Let
.
Let
![]() be the Tamagawa
number of
be the Tamagawa
number of ![]() at
at ![]() .
The reduction of
.
The reduction of ![]() lies in the identity component
of the closed fiber
lies in the identity component
of the closed fiber
![]() of the Néron model of
of the Néron model of ![]() at
at ![]() , so by Lemma 3.4,
there exists
, so by Lemma 3.4,
there exists
![]() such that
such that ![]() .
Thus the cohomology class
.
Thus the cohomology class
![]() is defined by a cocycle that sends
is defined by a cocycle that sends
![]() to
to
![]() (see diagram (3.2) for the definition of
(see diagram (3.2) for the definition of ![]() ).
In particular,
).
In particular,
![]() is unramified at
is unramified at ![]() .
By [Mil86, Prop. 3.8],
.
By [Mil86, Prop. 3.8],
Case 3.
![]() :
Suppose that
:
Suppose that
![]() .
Let
.
Let ![]() be the ring of integers of
be the ring of integers of ![]() ,
and let
,
and let
![]() ,
,
![]() , and
, and
![]() be the
Néron models of
be the
Néron models of ![]() ,
, ![]() , and
, and ![]() , respectively.
Since
, respectively.
Since ![]() and
and ![]() has abelian reduction at
has abelian reduction at ![]() (since
(since ![]() ),
by [BLR90, Thm. 7.5.4(iii)],
the induced sequence
),
by [BLR90, Thm. 7.5.4(iii)],
the induced sequence
![]() is exact,
which means that
is exact,
which means that ![]() is faithfully flat
and surjective with scheme-theoretic
kernel
is faithfully flat
and surjective with scheme-theoretic
kernel
![]() . Since
. Since ![]() is faithfully flat with smooth kernel,
is faithfully flat with smooth kernel, ![]() is smooth (see, e.g., [BLR90, 2.4.8]).
By Lemma 3.6,
is smooth (see, e.g., [BLR90, 2.4.8]).
By Lemma 3.6,
![]() is a surjection; i.e.,
is a surjection; i.e.,
![]() is a surjection.
is a surjection.
So
![]() is
unramified, and again by
[Mil86, Prop. 3.8],
is
unramified, and again by
[Mil86, Prop. 3.8],