


Next: Visible Elements of
Up: Visibility of Shafarevich-Tate Groups
Previous: Introduction
Visibility
In Section 1.1 we introduce visible cohomology classes,
then in Section 1.2 we discuss visible elements of
Shafarevich-Tate groups. In Section 1.3, we use
restriction of scalars to deduce that every cohomology class is
visible somewhere.
For a field 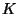 and a smooth commutative
and a smooth commutative 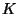 -group scheme
-group scheme 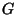 , we
write
, we
write 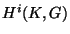 to denote the group cohomology
to denote the group cohomology
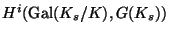 where
where 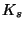 is a fixed separable closure
of
is a fixed separable closure
of 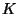 ; equivalently,
; equivalently, 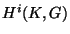 denotes the
denotes the 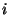 th étale
cohomology of
th étale
cohomology of 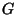 viewed as an étale sheaf on
viewed as an étale sheaf on
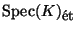 .
.
Subsections
William A Stein
2002-02-27
![]() and a smooth commutative
and a smooth commutative ![]() -group scheme
-group scheme ![]() , we
write
, we
write ![]() to denote the group cohomology
to denote the group cohomology
![]() where
where ![]() is a fixed separable closure
of
is a fixed separable closure
of ![]() ; equivalently,
; equivalently, ![]() denotes the
denotes the ![]() th étale
cohomology of
th étale
cohomology of ![]() viewed as an étale sheaf on
viewed as an étale sheaf on
![]() .
.