Proof of Theorem 3.10
Theorem 3.10 asserts that if 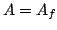 is a quotient of
is a quotient of 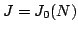 attached to a newform
attached to a newform 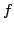 , and
, and 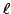 is a prime
such that
is a prime
such that
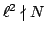 , then
, then
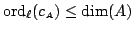 . Our proof follows [AU96],
except at the end we argue using lattice indices instead of multiples.
. Our proof follows [AU96],
except at the end we argue using lattice indices instead of multiples.
Let 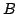 denote the kernel of the quotient map
denote the kernel of the quotient map
 .
Consider the exact sequence
.
Consider the exact sequence
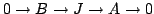 ,
and the corresponding complex
,
and the corresponding complex
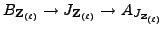 of Néron models. Because
of Néron models. Because
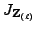 has
semiabelian reduction (since
has
semiabelian reduction (since
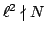 ), Theorem A.1 of the
appendix of [AU96, pg. 279-280], due to Raynaud,
implies that there is an
integer
), Theorem A.1 of the
appendix of [AU96, pg. 279-280], due to Raynaud,
implies that there is an
integer 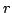 and an exact sequence
and an exact sequence
Here
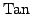 is the tangent space at the 0
section; it is a
finite free
is the tangent space at the 0
section; it is a
finite free
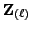 -module of rank equal to the dimension.
In particular, we have
-module of rank equal to the dimension.
In particular, we have
 .
Note that
.
Note that
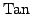 is
is
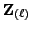 -dual to the cotangent
space, and the cotangent space is isomorphic to the space of global
differential
-dual to the cotangent
space, and the cotangent space is isomorphic to the space of global
differential 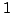 -forms. The theorem of Raynaud mentioned above is the
generalization to
-forms. The theorem of Raynaud mentioned above is the
generalization to 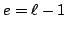 of [Maz78, Cor. 1.1], which we used
above in the proof of Theorem 3.5.
of [Maz78, Cor. 1.1], which we used
above in the proof of Theorem 3.5.
Let 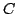 be the cokernel of
be the cokernel of
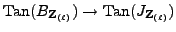 . We
have a diagram
. We
have a diagram
![$\displaystyle \xymatrix @=0.15in{ 0 \ar[r] & {{\mathrm{Tan}}(B_{{{\bf {Z}}_{(\e...
...)}\ar[r]& {({\bf {Z}}/{\ell}{\bf {Z}})^r}\ar[r]& 0. & & & C\ar@{^(->}[ru] }$](img359.png) |
(3) |
Since
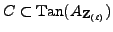 , so
, so 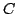 is torsion free, we see that
is torsion free, we see that 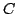 is a free
is a free
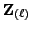 -module of rank
-module of rank 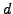 . Let
. Let
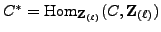 be the
be the
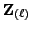 -linear dual of
-linear dual of 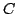 . Applying the
. Applying the
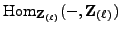 functor to the two short exact sequences in
(3), we obtain exact sequences
functor to the two short exact sequences in
(3), we obtain exact sequences
and
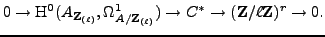 |
(4) |
The
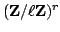 on the right in (4)
occurs as
on the right in (4)
occurs as
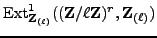 .
.
Since
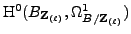 is
torsion free, by Lemma 4.1, the induced map
is
torsion free, by Lemma 4.1, the induced map
is injective.
Since 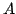 is a newform quotient, if
is a newform quotient, if
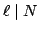 then
then
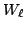 acts as a scalar on
acts as a scalar on 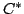 and on
and on
![$ S_2(\Gamma_0(N);{{{\bf {Z}}_{(\ell)}}})[I]$](img336.png) .
Using Lemma 4.2, with
.
Using Lemma 4.2, with 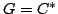 , we see that
the image of
, we see that
the image of 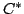 in
in
![$ {{\bf {Z}}_{(\ell)}}[[q]]$](img231.png) under the composite
of the maps in (1)
is saturated. The Manin
constant for
under the composite
of the maps in (1)
is saturated. The Manin
constant for 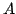 at
at 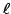 is the index
of the image via
is the index
of the image via 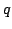 -expansion of
-expansion of
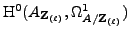 in
in
![$ {{\bf {Z}}_{(\ell)}}[[q]]$](img231.png) in its saturation. Since the image of
in its saturation. Since the image of 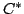 in
in
![$ {{\bf {Z}}_{(\ell)}}[[q]]$](img231.png) is saturated, the image of
is saturated, the image of 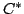 is the saturation of the image
of
is the saturation of the image
of
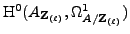 , so the Manin constant
at
, so the Manin constant
at 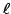 is the
index of
is the
index of
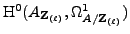 in
in 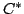 , which is
, which is 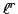 by (4), hence is
at most
by (4), hence is
at most 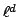 .
.
William Stein
2006-06-25
![]() denote the kernel of the quotient map
denote the kernel of the quotient map
![]() .
Consider the exact sequence
.
Consider the exact sequence
![]() ,
and the corresponding complex
,
and the corresponding complex
![]() of Néron models. Because
of Néron models. Because
![]() has
semiabelian reduction (since
has
semiabelian reduction (since
![]() ), Theorem A.1 of the
appendix of [AU96, pg. 279-280], due to Raynaud,
implies that there is an
integer
), Theorem A.1 of the
appendix of [AU96, pg. 279-280], due to Raynaud,
implies that there is an
integer ![]() and an exact sequence
and an exact sequence
![]() be the cokernel of
be the cokernel of
![]() . We
have a diagram
. We
have a diagram
![]() is
torsion free, by Lemma 4.1, the induced map
is
torsion free, by Lemma 4.1, the induced map