-
- AU96
-
A. Abbes and E. Ullmo, À propos de la conjecture de Manin pour les
courbes elliptiques modulaires, Compositio Math. 103 (1996), no. 3,
269-286.
- Aga99
-
A. Agashe, On invisible elements of the Tate-Shafarevich group, C.
R. Acad. Sci. Paris Sér. I Math. 328 (1999), no. 5, 369-374.
- Aga00
-
A. Agashe, The Birch and Swinnerton-Dyer formula for modular
abelian varieties of analytic rank zero, Ph.D. thesis, University of
California, Berkeley (2000),
http://www.math.missouri.edu/~ agashe/math.html/.
- AL70
-
A.O.L. Atkin and J. Lehner, Hecke operators on
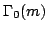 , Math. Ann. 185 (1970), 134-160.
, Math. Ann. 185 (1970), 134-160.
- ARS
-
A. Agashe, K. Ribet, and W.A. Stein, The modular degree,
congruence primes, and multiplicity one (2005).
- AS05
-
A. Agashe and W.A. Stein, Visible evidence for the Birch and
Swinnerton-Dyer conjecture for modular abelian varieties of analytic rank
zero, Math. Comp. 74 (2005), no. 249, 455-484, with
an appendix by J. Cremona and B. Mazur.
- BLR90
-
S. Bosch, W. Lütkebohmert, and M. Raynaud, Néron models,
Springer-Verlag, Berlin, 1990.
- BCDT01
-
C. Breuil, B. Conrad, F. Diamond, and R. Taylor, On the modularity of
elliptic curves over
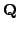 : wild 3-adic exercises, J. Amer. Math. Soc.
14 (2001), no. 4, 843-939 (electronic).
: wild 3-adic exercises, J. Amer. Math. Soc.
14 (2001), no. 4, 843-939 (electronic).
- BF01
-
D. Burns and M. Flach, Tamagawa numbers for motives with
(non-commutative) coefficients, Doc. Math. 6 (2001), 501-570
(electronic).
- CE05
-
F. Calegari and M. Emerton, Elliptic curves of odd modular degree,
Preprint (2005).
- CES03
-
B. Conrad, S. Edixhoven, and W.A. Stein,
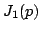 Has
Connected Fibers, Documenta Mathematica 8 (2003), 331-408.
Has
Connected Fibers, Documenta Mathematica 8 (2003), 331-408.
- Cre97
-
J.E. Cremona, Algorithms for modular elliptic curves, second
ed., Cambridge University Press, Cambridge, 1997,
http://www.maths.nott.ac.uk/personal/jec/book/.
- Cre
-
J.E. Cremona, Tables of Elliptic Curves,
http://www.maths.nott.ac.uk/personal/jec/ftp/data/.
- DI95
-
F. Diamond and J. Im, Modular forms and modular curves, Seminar on
Fermat's Last Theorem (Toronto, ON, 1993-1994), Amer. Math. Soc.,
Providence, RI, 1995, pp. 39-133.
- DR73
-
P. Deligne and M. Rapoport, Les schémas de modules de courbes
elliptiques, Modular functions of one variable, II (Proc. Internat. Summer
School, Univ. Antwerp, Antwerp, 1972) (Berlin), Springer, 1973, pp. 143-316.
Lecture Notes in Math., Vol. 349.
- Edi89
-
B. Edixhoven, Stable models of modular curves and applications, Thèse
de doctorat à l'université d'Utrecht (1989),
http://www.maths.univ-rennes1.fr/~ edix/publications/
prschr.html/.
- Edi91
-
B. Edixhoven, On the Manin constants of modular elliptic curves,
Arithmetic algebraic geometry (Texel, 1989), Birkhäuser Boston, Boston, MA,
1991, pp. 25-39.
- FpS+01
-
E.V. Flynn, F. Leprévost, E.F. Schaefer,
W.A. Stein, M. Stoll, and J.L. Wetherell,
Empirical evidence for the Birch and Swinnerton-Dyer conjectures
for modular Jacobians of genus 2 curves, Math. Comp. 70 (2001),
no. 236, 1675-1697 (electronic).
- GL01
-
Josep González and Joan-C. Lario,
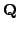 -curves and their
Manin ideals, Amer. J. Math. 123 (2001), no. 3, 475-503.
-curves and their
Manin ideals, Amer. J. Math. 123 (2001), no. 3, 475-503.
- Gro82
-
B.H. Gross, On the conjecture of Birch and
Swinnerton-Dyer for elliptic curves with complex multiplication, Number
theory related to Fermat's last theorem (Cambridge, Mass., 1981),
Birkhäuser Boston, Mass., 1982, pp. 219-236.
- GZ86
-
B. Gross and D. Zagier, Heegner points and derivatives of
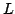 -series, Invent. Math. 84 (1986), no. 2, 225-320.
-series, Invent. Math. 84 (1986), no. 2, 225-320.
- Joy05
-
A. Joyce, The Manin constant of an optimal quotient of
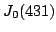 , J. Number Theory 110 (2005), no. 2, 325-330.
, J. Number Theory 110 (2005), no. 2, 325-330.
- Kil02
- L.J.P. Kilford,
Some non-Gorenstein Hecke algebras attached to spaces of
modular forms, J. Number Theory 97 (2002), no. 1,
157-164.
- KM85
-
N.M. Katz and B. Mazur, Arithmetic moduli of elliptic
curves, Princeton University Press, Princeton, N.J., 1985.
- Lan91
-
S. Lang, Number theory. III, Springer-Verlag, Berlin, 1991,
Diophantine geometry.
- Man72
-
J.I. Manin, Parabolic points and zeta functions of modular
curves, Izv. Akad. Nauk SSSR Ser. Mat. 36 (1972), 19-66.
- Maz77
-
B. Mazur, Modular curves and the Eisenstein ideal, Inst.
Hautes Études Sci. Publ. Math. (1977), no. 47, 33-186 (1978).
- Maz78
-
B. Mazur, Rational isogenies of prime degree (with an appendix by D.
Goldfeld), Invent. Math. 44 (1978), no. 2, 129-162.
- MR91
-
B. Mazur and K.A. Ribet, Two-dimensional representations in
the arithmetic of modular curves, Astérisque (1991), no. 196-197, 6,
215-255 (1992), Courbes modulaires et courbes de Shimura (Orsay, 1987/1988).
- Mc91
-
W.G. McCallum, Kolyvagin's work on Shafarevich-Tate
groups,
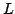 -functions and arithmetic (Durham, 1989), Cambridge Univ. Press,
Cambridge, 1991, pp. 295-316.
-functions and arithmetic (Durham, 1989), Cambridge Univ. Press,
Cambridge, 1991, pp. 295-316.
- Shi73
-
G. Shimura, On the factors of the jacobian variety of a modular function
field, J. Math. Soc. Japan 25 (1973), no. 3, 523-544.
- Shi94
-
G. Shimura, Introduction to the arithmetic theory of automorphic
functions, Princeton University Press, Princeton, NJ, 1994, Reprint of the
1971 original, Kan Memorial Lectures, 1.
- Sil92
-
J.H. Silverman, The arithmetic of elliptic curves,
Springer-Verlag, New York, 1992, Corrected reprint of the 1986 original.
- Sil94
-
J.H. Silverman, Advanced topics in the arithmetic of elliptic
curves, Springer-Verlag, New York, 1994.
- SW04
-
W. Stein and M. Watkins, Modular parametrizations of
Neumann-Setzer elliptic curves, Int. Math. Res. Not. (2004), no. 27,
1395-1405.
- Ste89
-
G. Stevens, Stickelberger elements and modular parametrizations of
elliptic curves, Invent. Math. 98 (1989), no. 1, 75-106.
- Vat05
-
V. Vatsal, Multiplicative subgroups of
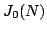 and applications to
elliptic curves, J. Inst. Math. Jussieu 4 (2005), no. 2, 281-316.
and applications to
elliptic curves, J. Inst. Math. Jussieu 4 (2005), no. 2, 281-316.
William Stein
2006-06-25