Proof of Theorem 3.11
We continue to use the notation and hypotheses of Section 4.1
(so
 )
and assume in addition that
)
and assume in addition that 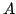 is a newform quotient, and
that
is a newform quotient, and
that
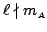 . We have to show that then
. We have to show that then
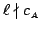 .
Just as in the previous proof,
it suffices to check that the image of
.
Just as in the previous proof,
it suffices to check that the image of
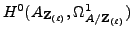 in
in
![$ {{{\bf {Z}}_{(\ell)}}}[[q]]$](img258.png) is saturated.
Since
is saturated.
Since 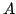 is a newform quotient, if
is a newform quotient, if
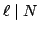 , then
, then
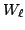 acts as a scalar on
acts as a scalar on 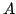 and on
and on
![$ S_2(\Gamma_0(N);{{{\bf {Z}}_{(\ell)}}})[I]$](img336.png) .
So again, using Lemma 4.2,
it suffices to show that the map
.
So again, using Lemma 4.2,
it suffices to show that the map
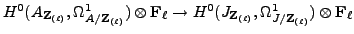 is injective.
is injective.
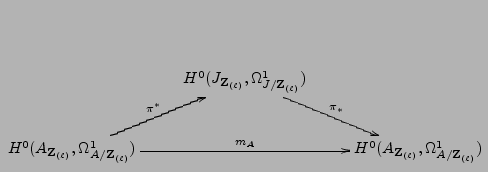
The composition of pullback and pushforward in the following diagram
is multiplication by the modular exponent of 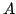 :
:
Since
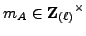 , the map
, the map 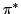 is a
section to the map
is a
section to the map
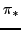 up to a unit and hence its reduction modulo
up to a unit and hence its reduction modulo 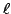 is
injective, which is what was left to be shown.
Let tex2html_wrap_inline$&pi#pi;_*$ and tex2html_wrap_inline$&pi#pi;^*$denote the maps obtained by tensoring the diagram above with
tex2html_wrap_inline$F_&ell#ell;$. Then tex2html_wrap_inline$&pi#pi;_*&cir#circ;&pi#pi;^*$ is
multiplication by an integer coprime to tex2html_wrap_inline$&ell#ell;$ from the finite dimension
tex2html_wrap_inline$F_&ell#ell;$-vector space tex2html_wrap_inline$H^0(A_Z_(&ell#ell;), &Omega#Omega;^1_A/Z_(&ell#ell;))&otimes#otimes;F_&ell#ell;$ to
itself, hence an isomorphism. In particular, tex2html_wrap_inline$&pi#pi;^*$ is
injective, which is what was left to show.
is
injective, which is what was left to be shown.
Let tex2html_wrap_inline$&pi#pi;_*$ and tex2html_wrap_inline$&pi#pi;^*$denote the maps obtained by tensoring the diagram above with
tex2html_wrap_inline$F_&ell#ell;$. Then tex2html_wrap_inline$&pi#pi;_*&cir#circ;&pi#pi;^*$ is
multiplication by an integer coprime to tex2html_wrap_inline$&ell#ell;$ from the finite dimension
tex2html_wrap_inline$F_&ell#ell;$-vector space tex2html_wrap_inline$H^0(A_Z_(&ell#ell;), &Omega#Omega;^1_A/Z_(&ell#ell;))&otimes#otimes;F_&ell#ell;$ to
itself, hence an isomorphism. In particular, tex2html_wrap_inline$&pi#pi;^*$ is
injective, which is what was left to show.
theorem_type[rmk][lem][][definition][][]
Adam Joyce observed that one can also obtain injectivity
of tex2html_wrap_inline$&pi#pi;^*$ as a
consequence of Prop. 7.5.3(a) of [BLR90].
William Stein
2006-06-25
![]() :
: