The following is a general bound on the visibility dimension.
Proof.
The map
![$ H^1(K,A[n])\rightarrow H^1(K,A)[n]$](img74.png)
is surjective
and
![$ A[n]$](img75.png)
has order
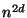
,
so
Lemma
2.2 implies that there is an extension
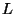
of
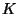
of degree at most
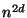
such that
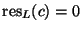
.
The proof of Proposition
1.3 implies
that
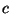
is visible in an abelian variety of dimension
![$ [L:K]\cdot \dim A\leq d n^{2d}$](img77.png)
.
