The Smallest Conductor for an Elliptic Curve of Rank Four is Composite
August 20, 2003
Introduction
If E is an elliptic curve over Q in Weierstrass
normal form y² = x³ + ax + b, then the
set
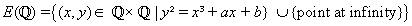
has a natural structure of finitely-generated abelian group,
which can be decomposed as 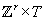 , where
T is a finite abelian group and r is greater than or equal to
0. This r is called the rank of the curve.
, where
T is a finite abelian group and r is greater than or equal to
0. This r is called the rank of the curve.
The conductor N of an elliptic curve is an integer
attached to the elliptic curve which measures the extent to which E fails
to define an elliptic curve over Fp for each prime p.
The conductor has the following important properties:
Thus, for any positive integer r, the following question
can be answered in a finite amount of time:
Question 1. What the smallest N for which there is an elliptic
curve of conductor N and rank r?
The smallest conductors for r = 0,1,2,3 are known:
| r |
smallest conductor |
an E of conductor N and rank r |
| 0 |
11 |
y² + y = x³ - x²
|
| 1 |
37 |
y² + y = x³ - x
|
| 2 |
389 |
y² + y = x³ +x² - 2x
|
| 3 |
5077 |
y² + y = x³ - 7x + 6
|
The answer is not known with certainty for any r larger than 3. Tom
Womack is maintaining a table
of the current status of this problem. Below is a graph of the known conductors
and ranks of the associated elliptic curves:
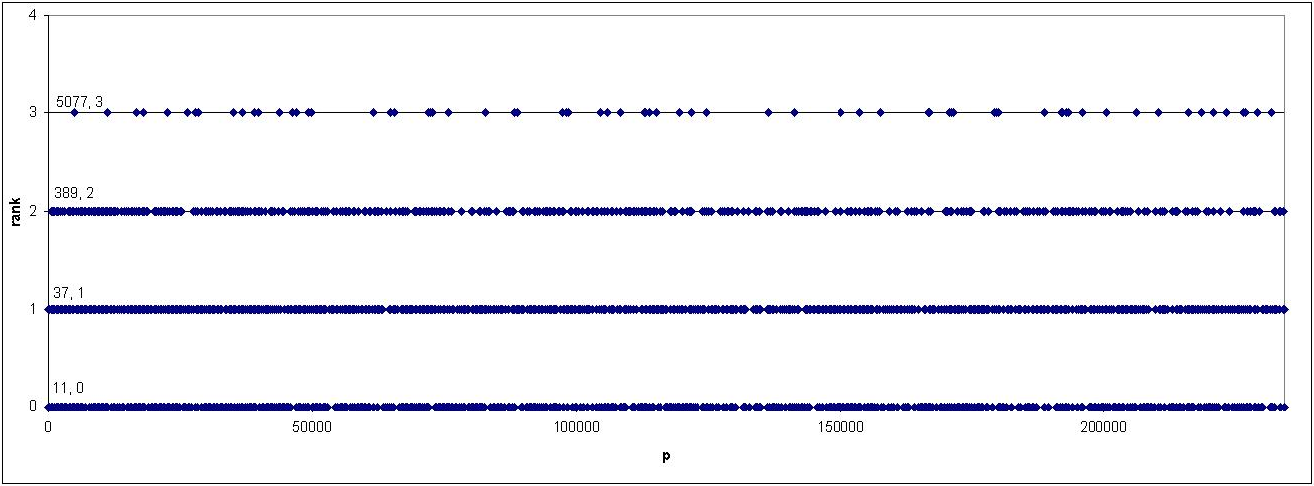
The current smallest known conductors (as of August 2003) for curves
of ranks 4, 5, and 6 are given in the following table:
| r |
smallest known conductor |
an E of conductor N and rank r |
| 4 |
2 · 117223
|
y² + xy = x³ - x² - 79x
+ 289
|
| 5 |
19047851
|
y² + y = x³ - 79x + 342
|
| 6 |
2 · 3 · 2777 · 311341
|
y² + xy = x³ +x² - 2582x +48720
|
Notice that the smallest conductors for ranks r less than 4 are all
prime. Up until August of 2003, the smallest known conductor of a curve of
rank 4 was the composite 2 · 117223 = 234446. There are 20782 primes
less than 234446, the largest of these being 234431. This motivated our investigation:
Question 2. Is there an elliptic curve of prime conductor
less than or equal to 234431 wtih rank 4?
Much groundwork in this area was laid in the works of Brumer-McGuinness
and Stein-Watkins.
Our project concerns the implementation of an algorithm due to Mestre
and Oesterle that can be used to quickly find all the elliptic curves
of prime conductor p.
Citations
algorithm due to Manin and Birch: see Cremona's Algorithms
for Modular Elliptic Curves for a description
algorithm due to Mestre and Oesterle: paper available
![]()
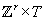 , where
T is a finite abelian group and r is greater than or equal to
0. This r is called the rank of the curve.
, where
T is a finite abelian group and r is greater than or equal to
0. This r is called the rank of the curve. 