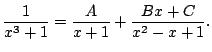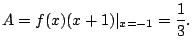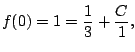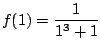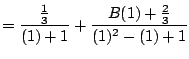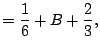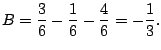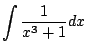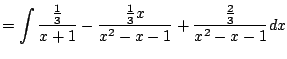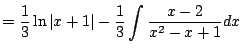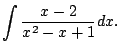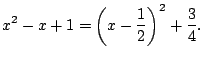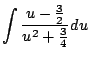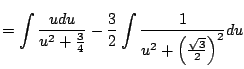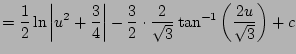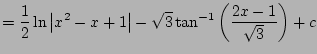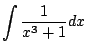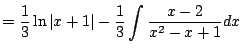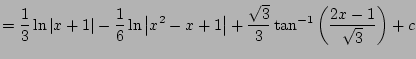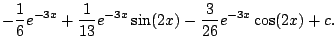Today: 7.4: Integration of rational functions and
Supp. 4: Partial fraction expansion
Next: 7.7: Approximate integration |
Our goal today is to compute integrals of
the form
by decomposing
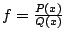 .
This is called partial fraction expansion.
.
This is called partial fraction expansion.
Note that
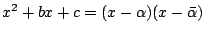 , where
, where
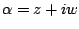 ,
,
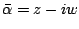 are complex conjugates.
are complex conjugates.
Types of rational functions
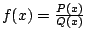 . To do a
partial fraction expansion, first make sure
. To do a
partial fraction expansion, first make sure
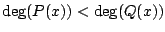 using long division. Then there are four possible situation,
each of increasing generality (and difficulty):
using long division. Then there are four possible situation,
each of increasing generality (and difficulty):
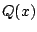 is a product of distinct linear factors;
is a product of distinct linear factors;
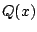 is a product of linear factors, some of which are repeated;
is a product of linear factors, some of which are repeated;
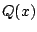 is a product of distinct irreducible quadratic factors,
along with linear factors some of which may be repeated; and,
is a product of distinct irreducible quadratic factors,
along with linear factors some of which may be repeated; and,
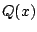 is has repeated irreducible quadratic factors, along with
possibly some linear factors which may be repeated.
is has repeated irreducible quadratic factors, along with
possibly some linear factors which may be repeated.
The general partial fraction expansion theorem is beyond the
scope of this course. However, you might find the following
special case and its proof interesting.
Proof.
Since
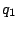
and
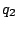
are relatively prime, using the Euclidean
algorithm (long division), we can find polynomials
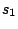
and
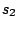
such that
Dividing both sides by
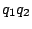
and multiplying by
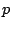
yields
which completes the proof.

Example 5.5.3
Compute
First do long division. Get quotient of
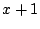
and remainder of
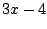
.
This means that
Since we have distinct linear factors, we know
that we can write
for real numbers
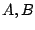
.
A clever way to find
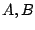
is to substitute
appropriate values in, as follows.
We have
Setting
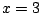
on both sides we have (taking a limit):
Likewise, we have
Thus
Example 5.5.4
Compute the partial fraction expansion of
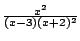
.
By the partial fraction theorem, there are constants
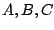
such that
Note that there's no possible way this could work
without the
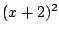
term, since otherwise
the common denominator would be
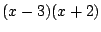
.
We have
This method will not get us
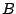
!
For example,
While true this is useless.
Instead, we use that we know 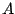 and
and 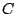 ,
and evaluate at another value of
,
and evaluate at another value of 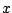 , say 0.
, say 0.
so
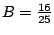
.
Thus finally,
Example 5.5.5
Let's compute
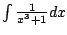
.
Notice that
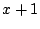
is a factor, since
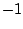
is a root.
We have
There exist constants
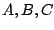
such that
Then
You could find
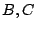
by factoring the quadratic over
the complex numbers and getting complex number
answers. Instead, we evaluate
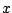
at a couple of values.
For example, at
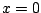
we get
so
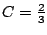
.
Next, use
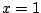
to get
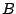
.
so
Finally,
It remains to compute
First, complete the square to get
Let
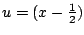
, so
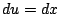
and
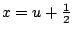
.
Then
Finally, we put it all together and get
| Discuss second quiz problem.
Problem: Compute
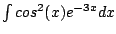 using
complex exponentials.
The answer is using
complex exponentials.
The answer is
Here's how to get it.
Simplify the inside part requires some imagination:
|
William Stein
2006-03-15
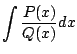
![]() , where
, where
![]() ,
,
![]() are complex conjugates.
are complex conjugates.
![]() . To do a
partial fraction expansion, first make sure
. To do a
partial fraction expansion, first make sure
![]() using long division. Then there are four possible situation,
each of increasing generality (and difficulty):
using long division. Then there are four possible situation,
each of increasing generality (and difficulty):
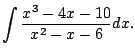
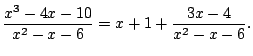
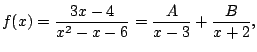
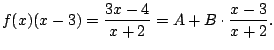
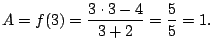
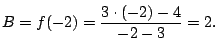
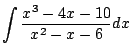
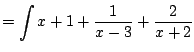
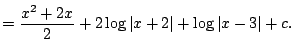
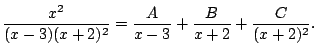
![$\displaystyle = \left[ f(x) (x-3)\right]_{x=3} = \frac{x^2}{(x+2)^2}\vert _{x=3} = \frac{9}{25},$](img764.png)
![$\displaystyle = \left[ f(x) (x+2)^2\right]_{x=-2} = -\frac{4}{5}.$](img766.png)
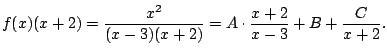
![]() and
and ![]() ,
and evaluate at another value of
,
and evaluate at another value of ![]() , say 0.
, say 0.
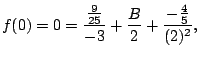
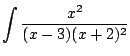
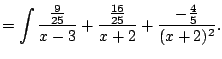
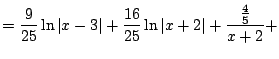 constant
constant