Next: Integration of Rational Functions Up: Integration Techniques Previous: Trigonometric Substitutions Contents Index
| Quizes today! |
How do you compute something like
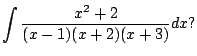
But how on earth do you right the rational function on the left hand side as a sum of the nice terms of the right hand side? Doing this is called ``partial fraction decomposition'', and it is a fundamental idea in mathematics. It relies on our ability to factor polynomials and saolve linear equations. As a first hint, notice that
Before describing the secret behind (5.4.1), we'll discuss some background about how polynomials and rational functions work.
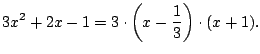
If ![]() is a polynomial, the roots
is a polynomial, the roots ![]() of
of ![]() correspond to the factors of
correspond to the factors of ![]() . Thus if
. Thus if
For example,
For example, for (5.4.2) the poles
are at ![]() ,
, ![]() , and
, and ![]() . They have
multiplicity
. They have
multiplicity ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
William Stein 2006-03-15