Next: Improper Integrals Up: Integration Techniques Previous: Integration of Rational Functions Contents Index
| Today: 7.7 - approximating integrals
Friday: Third QUIZ and 7.8 - improper integrals |
Problem: Compute
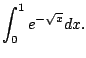
Today we will revisit Riemann sums in the context
of finding numerical approximations to integrals,
which we might not be able to compute exactly.
Recall that if ![]() then
then
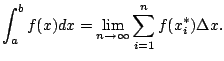
For example, we could use Riemann sums to approximate
![]() ,
say using left endpoints. This gives the approximation:
,
say using left endpoints. This gives the approximation:
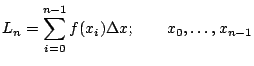 left endpoints
left endpoints
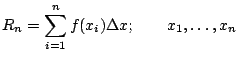 right endpoints
right endpoints
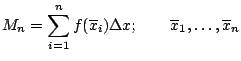 midpoints
midpointsYet another possibility is the trapezoid approximation, which is
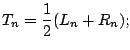
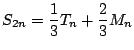
Many functions have no elementary antiderivatives:
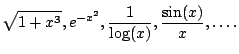
Some of these functions are extremly important. For example, the
integrals
![]() are extremely important in
probability, even though there is no simple formula for the
antiderivative.
are extremely important in
probability, even though there is no simple formula for the
antiderivative.
If you are doing scientific research you might spend months
tediously computing values of some function ![]() , for which no
formula is known.
, for which no
formula is known.
The following is a table of the values
of ![]() at
at ![]() for
for
![]() .
.
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
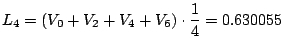
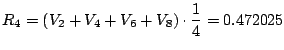
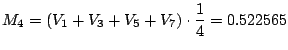
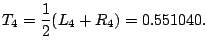
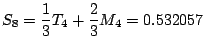
Maxima gives
![]() and
Mathematica gives
and
Mathematica gives ![]() .
.
Note that Simpsons's is the best; it better be, since we worked the hardest to get it!
| Method | Error |
| 0.101573 | |
| 0.056458 | |
| 0.005917 | |
|
|
0.022558 |
|
|
0.003575 |
William Stein 2006-03-15