Next: Complex Exponentials and Trig Up: Complex Numbers Previous: Complex Numbers Contents Index
NOTE: The ``existence'' of complex numbers wasn't generally accepted until people got used to a geometric interpretation of them.
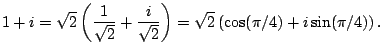
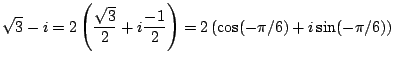
Finding the polar form of a complex number is exactly
the same problem as finding polar coordinates of a point
in rectangular coordinates. The only hard part is figuring
out what ![]() is.
is.
If we write complex numbers in rectangular form, their sum is easy to compute:
For example, the power of a singular complex number in polar
form is easy to compute; just power the ![]() and multiply
the angle.
and multiply
the angle.
| EXAM 1: Wednesday 7:00-7:50pm in Pepper Canyon 109 (!)
Today: Supplement 1 (get online; also homework online) Wednesday: Review Bulletin board, online chat, directory, etc. - see main course website. Review day - I will prepare no LECTURE; instead I will answer questions. Your job is to have your most urgent questions ready to go! Office hours moved: NOT Tue 11-1 (since nobody ever comes then and I'll be at a conference); instead I'll be in my office to answer questions WED 1:30-4pm, and after class on WED too. Office: AP&M 5111 |
| Quick review:
Given a point
Theorem 4.3.6 (De Moivre's)
For any integer
|
Since we know how to raise a complex number in polar form
to the ![]() th power, we can find all numbers with a given
power, hence find the
th power, we can find all numbers with a given
power, hence find the ![]() th roots of a complex number.
th roots of a complex number.
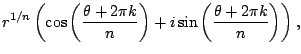
An application of De Moivre is to computing
![]() and
and
![]() in terms of
in terms of
![]() and
and
![]() . For example,
. For example,
William Stein 2006-03-15