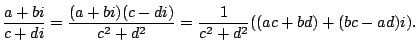A complex number is an expression of the form
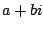 , where
, where 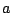 and
and 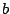 are real numbers,
and
are real numbers,
and 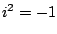 . We add and multiply
complex numbers as follows:
. We add and multiply
complex numbers as follows:
The complex conjugate of a complex number is
Note that
is a real number (has no complex part).
If
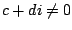 , then
, then
Example 4.3.1
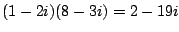
and
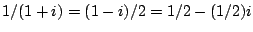
.
Complex numbers are incredibly useful in providing better
ways to understand ideas in calculus, and more generally
in many applications (e.g., electrical engineering,
quantum mechanics, fractals, etc.). For example,
- Every polynomial
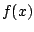 factors as a product
of linear factors
factors as a product
of linear factors
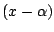 , if we allow the
, if we allow the
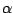 's in the factorization to be complex numbers.
For example,
This will provide an easier to use variant of
the ``partial fractions'' integration technique,
which we will see later.
's in the factorization to be complex numbers.
For example,
This will provide an easier to use variant of
the ``partial fractions'' integration technique,
which we will see later.
- Complex numbers are in correspondence with
points in the plane via
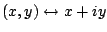 .
Via this correspondence we obtain a way to add and
multiply points in the plane.
.
Via this correspondence we obtain a way to add and
multiply points in the plane.
- Similarly, points in polar coordinates
correspond to complex numbers:
- Complex numbers provide a very nice way
to remember and understand trig identities.
Subsections
William Stein
2006-03-15
![]() , where
, where ![]() and
and ![]() are real numbers,
and
are real numbers,
and ![]() . We add and multiply
complex numbers as follows:
. We add and multiply
complex numbers as follows:
![]() , then
, then