Recall that
The angles add. You've seen something similar before:
This connection between exponentiation and (4.4)
gives us an idea!
If 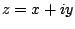 is a complex number, define
is a complex number, define
We have just written polar coordinates in another form. It's
a shorthand for the polar form of a complex number:
Theorem 4.4.1
If 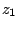 ,
, 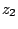 are two complex numbers, then
are two complex numbers, then
Proof.
Here we have just used (
4.4).

The following theorem is amazing, since it involves calculus.
Theorem 4.4.2
If 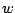 is a complex number, then
for
is a complex number, then
for 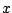 real. In fact, this is even true for
real. In fact, this is even true for
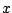 a complex variable (but we haven't defined differentiation
for complex variables yet).
a complex variable (but we haven't defined differentiation
for complex variables yet).
Proof.
Write
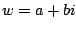
.
Now we use the product rule to get
On the other hand,
Wow!! We did it!

That Theorem 4.4.2 is true is pretty amazing. It's
what really gets complex analysis going.
Example 4.4.3
Here's another fun fact:
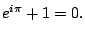 Solution.
Solution. By definition,
have
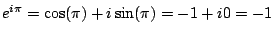
.
Subsections
William Stein
2006-03-15
![]() is a complex number, define
is a complex number, define
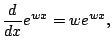
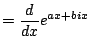
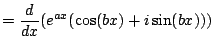
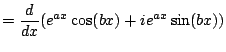
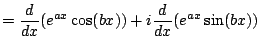
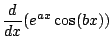
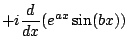
![]()