Next: Kolyvagin's Conjectures Up: Kolyvagin's Euler System Previous: Kolyvagin's Euler System Contents Index
We will use, when possible, similar notation to the notation
Kolyvagin uses in his papers (e.g.,
[Kol91]). If ![]() is an abelian group let
is an abelian group let
![]() . Kolyvagin writes
. Kolyvagin writes ![]() for the
for the ![]() -torsion subgroup,
but we will instead write
-torsion subgroup,
but we will instead write ![]() for this group.
for this group.
Let ![]() be an elliptic curve over
be an elliptic curve over ![]() with no constraint
on the rank of
with no constraint
on the rank of ![]() .
Fix a modular parametrization
.
Fix a modular parametrization
![]() , where
, where ![]() is the conductor of
is the conductor of ![]() .
Let
.
Let ![]() be a quadratic imaginary field with discriminant
be a quadratic imaginary field with discriminant ![]() that satisfies the Heegner hypothesis for
that satisfies the Heegner hypothesis for ![]() , so each
prime dividing
, so each
prime dividing ![]() splits in
splits in ![]() ,
and assume for simplicity that
,
and assume for simplicity that ![]() .
.
Let ![]() be the ring of integer of
be the ring of integer of ![]() . Since
. Since ![]() satisfies the
Heegner hypothesis, there is an ideal
satisfies the
Heegner hypothesis, there is an ideal ![]() in
in ![]() such that
such that
![]() is cyclic of order
is cyclic of order ![]() . For any positive integer
. For any positive integer
![]() , let
, let ![]() be the ray class field of
be the ray class field of ![]() associated to the conductor
associated to the conductor ![]() (see Definition 3.13).
Recall that
(see Definition 3.13).
Recall that ![]() is an abelian extension of
is an abelian extension of ![]() that is unramified outside
that is unramified outside ![]() , whose existence is
guaranteed by class field theory.
Let
, whose existence is
guaranteed by class field theory.
Let
![]() be the order in
be the order in ![]() of conductor
of conductor ![]() , and let
, and let
![]() .
Let
.
Let
Let
![]() , and
let
, and
let ![]() be the set of primes
be the set of primes ![]() in
in ![]() that do not divide the discriminant of
that do not divide the discriminant of ![]() and
are such that the image of the representation
and
are such that the image of the representation
sage: E = EllipticCurve('11a')
sage: E.non_surjective()
[(5, '5-torsion')]
sage: E = EllipticCurve('389a')
sage: E.non_surjective()
[]
Fix a prime ![]() . We next introduce some
very useful notation. Let
. We next introduce some
very useful notation. Let ![]() denote the set of all
primes
denote the set of all
primes
![]() such that
such that ![]() ,
, ![]() remains prime in
remains prime in ![]() ,
and for which
,
and for which
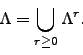
Fix an element
![]() , with
, with ![]() , and
consider the
, and
consider the ![]() -power
-power
If ![]() is any Galois extension, we have
(see Section 2.1.2 for most of this)
an exact sequence
is any Galois extension, we have
(see Section 2.1.2 for most of this)
an exact sequence
 = 0$.
(Compare \cite[Lem. 4.3]{gross:kolyvagin}.)
\end{proof}](img702.png)
Thus (3.4.1) with ![]() becomes
becomes
![\begin{displaymath}
\xymatrix{
0 \ar[r]& {(E(K_{\lambda})/M)^{G_{\lambda}}} \ar...
... 0\\
& & & \H ^1(K_\lambda/K, E)[M]\ar@{^(->}[u]^{\inf}\\
}
\end{displaymath}](img706.png)
Thus to construct
![]() , it suffices
to construct a class
, it suffices
to construct a class
![]() that is invariant under the action of
that is invariant under the action of ![]() .
We will do this by constructing an element of
.
We will do this by constructing an element of
![]() and using the inclusion
and using the inclusion
Recall that
![]() . Unfortunately,
there is no reason that the class
. Unfortunately,
there is no reason that the class
Let ![]() be the Hilbert class field of
be the Hilbert class field of ![]() .
Write
.
Write
![]() , and for each
, and for each ![]() let
let
![]() where
where ![]() is the ray class
field associated to
is the ray class
field associated to ![]() . Class field theory implies
that the natural map
. Class field theory implies
that the natural map
![\begin{displaymath}
\Tr _{p} = \sum_{\sigma \in G_{p}} \sigma \in \mathbb{Z}[G_{p}].
\end{displaymath}](img725.png)
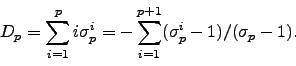
Finally, let ![]() be a set of coset representatives
for
be a set of coset representatives
for
![]() in
in
![]() ,
and let
,
and let
![\begin{displaymath}
J_{\lambda} = \sum_{\sigma \in S} \sigma \in \mathbb{Z}[G_{\lambda}].
\end{displaymath}](img733.png)
Let
Before proving that we can use ![]() to define
a cohomology class in
to define
a cohomology class in ![]() , we state two
crucial facts about the structure of the Heegner points
, we state two
crucial facts about the structure of the Heegner points ![]() .
.
We have now constructed an element of
![]() that is fixed by
that is fixed by ![]() . Via (3.4.3)
this defines an element
. Via (3.4.3)
this defines an element
![]() .
But then using (3.4.2) we obtain our
sought after class
.
But then using (3.4.2) we obtain our
sought after class
![]() .
.
We will also be interested in the image ![]() of
of ![]() in
in ![]() .
.
![\begin{proof}
% latex2html id marker 7874If $v$ is archimedean we are done, s...
...component. (See \cite[Prop. 6.2]{gross:kolyvagin} for
more details.)
\end{proof}](img761.png)
![\begin{proof}
See \cite[Prop. 6.2]{gross:kolyvagin} for the case $M=\ell$. The
a...
...diagram chasing, reduction
modulo a prime, and use of formal groups.
\end{proof}](img770.png)
Next we consider a consequence of Proposition 3.27
when ![]() is not a torsion point. Note that
is not a torsion point. Note that ![]() nontorsion implies
that
nontorsion implies
that
![]() for all but finitely many
for all but finitely many ![]() . Moreover,
the Gross-Zagier theorem implies that
. Moreover,
the Gross-Zagier theorem implies that ![]() is nontorsion if and only if
is nontorsion if and only if
![]() .
.

After Kolyvagin proved his theorem, independently
Murty-Murty, Bump-Friedberg-Hoffstein, Waldspurger,
each proved that infinitely many such quadratic imaginary
![]() always exists so long as
always exists so long as ![]() has analytic rank
has analytic rank ![]() or
or ![]() . Also, Taylor and Wiles proved
that every
. Also, Taylor and Wiles proved
that every ![]() over
over ![]() is modular. Thus we have
the following theorem:
is modular. Thus we have
the following theorem:
The author has computed the upper bound of the theorem
for all elliptic curves with conductor up to ![]() and
and
![]() .
.
William 2007-05-25