The inf-res Sequence
Suppose 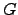 is a group and
is a group and 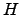 is a normal subgroup
of
is a normal subgroup
of 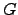 , and
, and 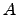 is a
is a 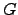 -module.
Then for any
-module.
Then for any 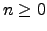 ,
there are natural homomorphisms
,
there are natural homomorphisms
and
Require that we view 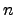 -cocycles as
certain maps on the
-cocycles as
certain maps on the 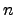 -fold product
of the group.
On cocycles, the map
-fold product
of the group.
On cocycles, the map 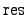 is
obtained by simply restricting
a cocycle, which is a map
is
obtained by simply restricting
a cocycle, which is a map 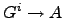 ,
to a map
,
to a map 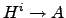 .
The second map
.
The second map 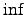 is obtained
by precomposing a cocycle
is obtained
by precomposing a cocycle
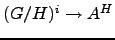 with the natural
map
with the natural
map
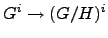 .
.
Proposition 2.4
The inf-res sequence
is exact.
![\begin{proof}
See \cite[\S{}VII.6]{serre:localfields}.
\end{proof}](img335.png)
William
2007-05-25