What about curves  with
with
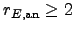 ? Suppose
that
? Suppose
that  is an elliptic curve over
is an elliptic curve over 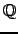 with
with
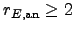 .
In the short paper [Kol91],
Kolyvagin states an amazing structure
theorems for Selmer groups assuming the following unproved conjecture,
which is the appropriate generalization of
the condition that
.
In the short paper [Kol91],
Kolyvagin states an amazing structure
theorems for Selmer groups assuming the following unproved conjecture,
which is the appropriate generalization of
the condition that 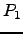 has infinite order.
has infinite order.
So far nobody has been able to show that Conjecture 3.32
is satisfied by every elliptic curve  over
over 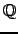 , though several
people are currently working hard on this problem (including
Vatsal and Cornut). Proposition 3.28
above implies that Conjecture 3.32 is true for
elliptic curves with
, though several
people are currently working hard on this problem (including
Vatsal and Cornut). Proposition 3.28
above implies that Conjecture 3.32 is true for
elliptic curves with
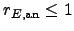 .
.
Kolyvagin also goes on in [Kol91]
to give a conjectural construction
of a subgroup
for which
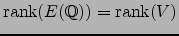 .
Let
.
Let 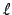 be an arbitrary prime, i.e., so we do not necessarily
assume
be an arbitrary prime, i.e., so we do not necessarily
assume 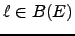 .
One can construct cohomology class
.
One can construct cohomology class
![$c_{\lambda} \in \H^1(K, E[M])$](img755.png) ,
so long as
,
so long as
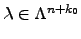 , where
, where
![$\ell^{k_0/2} E(\mathbf{K})[\ell^\infty] = 0$](img787.png) , and
, and
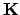 is the compositum of all class field
is the compositum of all class field 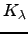 for
for
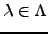 . For any
. For any 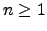 ,
,
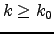 , and
, and 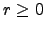 , let
, let
be the subgroup generated by the images of the
classes
![$\tau_{\lambda} = \tau_{\lambda,n}\in\H^1(K,E[\ell^n])$](img792.png) where
where 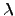 runs through
runs through
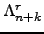 .
.
Recall that
and
Let 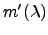 be the maximal nonnegative
integer such that
be the maximal nonnegative
integer such that
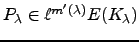 .
Let
.
Let
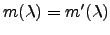 if
if
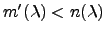 ,
and
,
and
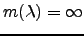 otherwise.
For any
otherwise.
For any 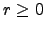 , let
, let
and let 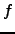 be the minimal
be the minimal 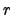 such that
such that 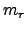 is finite.
is finite.
Proposition 3.34
We have 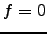 if and only if
if and only if 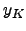 has infinite order.
has infinite order.
Let 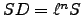 , where
, where
If
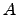 is a
is a
![$\mathbb{Z}[1,\sigma]$](img807.png) -module and
-module and
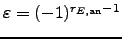 .
then
.
then
Assuming his conjectures, Kolyvagin deduces that
for every prime number 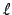 there exists
integers
there exists
integers 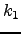 and
and 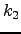 such that for
any integer
such that for
any integer 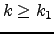 we have
we have
Here the exponent of 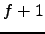 means the
means the 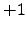 or
or 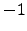 eigenspace
for the conjugation action.
eigenspace
for the conjugation action.
Conjecture 3.35 (Kolyvagin)
Let  be any elliptic curve over
be any elliptic curve over 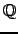 and
and 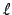 any prime.
There exists
any prime.
There exists 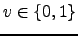 and a subgroup
such that
Let
and a subgroup
such that
Let
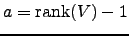 .
Then for all sufficiently large
.
Then for all sufficiently large 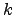 and all
and all 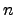 ,
one has that
,
one has that
Assuming the above conjecture for all primes 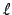 , the group
, the group 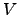 is
uniquely determined by the congruence condition in the second part of
the conjecture. Also, Kolyvagin proves that if the above conjecture
is true, then the rank of
is
uniquely determined by the congruence condition in the second part of
the conjecture. Also, Kolyvagin proves that if the above conjecture
is true, then the rank of
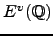 equals the rank of
equals the rank of 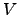 ,
and that
,
and that
![${\mbox{{\fontencoding{OT2}\fontfamily{wncyr}\fontseries{m}\fontshape{n}\selectfont Sh}}}(E^v/\mathbb{Q})[\ell^\infty]$](img824.png) is finite. (Here
is finite. (Here 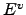 is
is  or its quadratic twist.)
or its quadratic twist.)
When 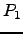 has infinite order, the conjecture is true
with
has infinite order, the conjecture is true
with 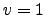 and
and
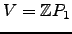 . (I think here
. (I think here  has
has
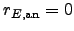 .)
.)
William
2007-05-25
![\begin{displaymath}
V_{n,k}^r \subset \varinjlim_{m}\H^1(K,E[\ell^m])/E(K)_{\tor }
\end{displaymath}](img791.png)
![]() , where
, where
![\begin{displaymath}
S = \varinjlim_{n} \Sel ^{(\ell^n)}(K,E[\ell^n]) .
\end{displaymath}](img806.png)
![]() there exists
integers
there exists
integers ![]() and
and ![]() such that for
any integer
such that for
any integer ![]() we have
we have
![]() , the group
, the group ![]() is
uniquely determined by the congruence condition in the second part of
the conjecture. Also, Kolyvagin proves that if the above conjecture
is true, then the rank of
is
uniquely determined by the congruence condition in the second part of
the conjecture. Also, Kolyvagin proves that if the above conjecture
is true, then the rank of
![]() equals the rank of
equals the rank of ![]() ,
and that
,
and that
![]() is finite. (Here
is finite. (Here ![]() is
is ![]() or its quadratic twist.)
or its quadratic twist.)
![]() has infinite order, the conjecture is true
with
has infinite order, the conjecture is true
with ![]() and
and
![]() . (I think here
. (I think here ![]() has
has
![]() .)
.)