next up previous
Next: Conjectures Up: Discriminants of Hecke Algebras Previous: Higher Weight Data

The Conjecture

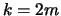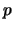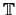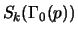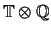Let $ k=2m$ be an even integer and $ p$ a prime. Let $ \mathbb{T}$ be the Hecke algebra associated to $ S_k(\Gamma_0(p))$ and let $ \tilde{\mathbb{T}}$ be the normalization of $ \tilde{\mathbb{T}}$ in $ \mathbb{T}\otimes \mathbb{Q}$.

Conjecture 5.1  

$\displaystyle \ord_p([\tilde{\mathbb{T}}: \mathbb{T}]) = \left\lfloor\frac{p}{12}\right\rfloor\cdot \binom{m}{2} + a(p,m), $

where

\begin{displaymath} a(p,m) = \begin{cases} 0 & \text{if $p\equiv 1\pmod{12}$,}... ... a(5,m)+a(7,m) & \text{if $p\equiv 11\pmod{12}$.} \end{cases}\end{displaymath}

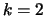
In particular, when $ k=2$ we conjecture that $ [\tilde{\mathbb{T}}:\mathbb{T}]$ is not divisible by $ p$.

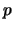
Here 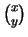$ \binom{x}{y}$ is the binomial coefficient ``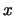$ x$ choose 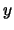$ y$'', and floor and ceiling are as usual. We have checked this conjecture against significant numerical data. (Will describe here.)


William A Stein 2002-09-30