


Next: About this document ...
Up: Discriminants of Hecke Algebras
Previous: The Conjecture
Conjecture 6.1
Suppose
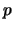
is a prime and
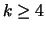
is an even integer.
If
then
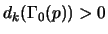
.
Frank Calegari outlined a possible strategy for proving this conjecture.
Conjecture 6.2
Suppose
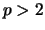
is a prime and
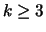
is an integer.
If
then
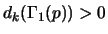
.
William A Stein
2002-09-30