The following are the valuations
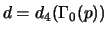 at
at 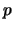 of the discriminant
of the Hecke algebras associated to
of the discriminant
of the Hecke algebras associated to
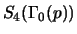 for
for 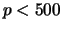 .
.
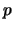 |
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
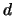 |
0 |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
4 |
4 |
6 |
6 |
6 |
6 |
8 |
8 |
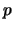 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
137 |
139 |
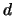 |
10 |
10 |
10 |
12 |
12 |
12 |
14 |
16 |
16 |
16 |
16 |
18 |
18 |
20 |
20 |
22 |
24 |
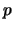 |
149 |
151 |
157 |
163 |
167 |
173 |
179 |
181 |
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
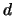 |
24 |
24 |
26 |
26 |
26 |
28 |
28 |
30 |
30 |
32 |
32 |
32 |
34 |
36 |
36 |
38 |
38 |
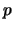 |
239 |
241 |
251 |
257 |
263 |
269 |
271 |
277 |
281 |
283 |
293 |
307 |
311 |
313 |
317 |
331 |
337 |
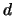 |
38 |
40 |
40 |
42 |
42 |
44 |
44 |
46 |
46 |
46 |
48 |
50 |
50 |
52 |
52 |
54 |
56 |
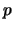 |
347 |
349 |
353 |
359 |
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
419 |
421 |
431 |
433 |
439 |
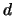 |
56 |
58 |
58 |
58 |
60 |
62 |
62 |
62 |
65 |
66 |
66 |
68 |
68 |
70 |
70 |
72 |
72 |
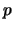 |
443 |
449 |
457 |
461 |
463 |
467 |
479 |
487 |
491 |
499 |
|
|
|
|
|
|
|
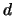 |
72 |
74 |
76 |
76 |
76 |
76 |
78 |
80 |
80 |
82 |
|
|
|
|
|
|
|
|
For each prime tex2html_wrap_inline$p$, let
displaymath
&delta#delta;(p) = S_4(&Gamma#Gamma;_0(p)) - S_p+3(&Gamma#Gamma;_0(1)).
Then tex2html_wrap_inline$|&delta#delta;(p) - d_4(&Gamma#Gamma;_0(p))| &le#leq;2$ for each tex2html_wrap_inline$p<500$.
Moreover, for every tex2html_wrap_inline$p&ne#neq;139$ we have that tex2html_wrap_inline$&delta#delta;(p)&ge#geq;
d_4(&Gamma#Gamma;_0(p))$, but for tex2html_wrap_inline$p=139$, tex2html_wrap_inline$&delta#delta;(p)=23$ but
tex2html_wrap_inline$d_4(&Gamma#Gamma;_0(p))=24$.