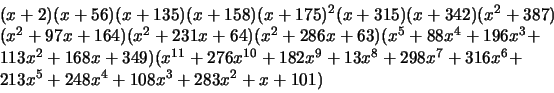Proposition 3.1
Suppose that
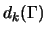
is finite.
Then the discriminant valuation
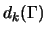
is nonzero
if and only if there is a mod-
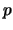
congruence
between two Hecke eigenforms in
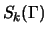
(note that the two congruent eigenforms might
be Galois conjugate).
Proof.
It follows from Proposition
2.2 that
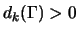
if and only if
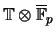
is not
separable. The Artinian ring
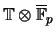
is
not separable if and only if the number of ring
homomorphisms
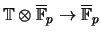
is
less than
Since
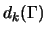
is finite, the number of ring
homomorphisms
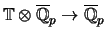
equals
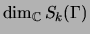
. Using the standard bijection between
congruences and normalized eigenforms, we see that
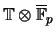
is not separable if and only
if there is a mod-
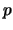
congruence between two eigenforms.

Example 3.2
If
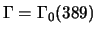
and
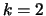
,
then
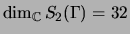
.
Let
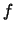
be the characteristic polynomial of
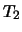
.
One can check that
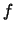
is square free and
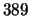
exactly
divides the discriminant of
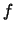
, so
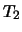
generated
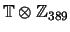
as a ring. (If it generated a subring of
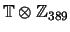
of finite index, then the discriminant of
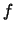
would be divisible
by
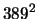
.)
Modulo 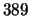 the polynomial
the polynomial 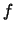 is congruent to
is congruent to
The factor
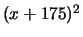
indicates that
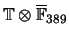
is not separable
since the image of
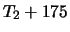
is nilpotent
(its square is 0). There are
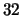
eigenforms over
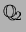
but only
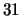
mod-
eigenforms, so there must be a congruence.
Let
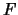
be the
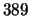
-adic newform whose
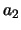
term is a root of
Then the congruence is between
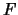
and its
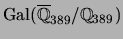
-conjugate.
Example 3.3
The discriminant of the Hecke algebra
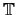
associated
to
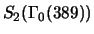
is
I computed this using the following algorithm, which was suggested
by Hendrik Lenstra. Using the Sturm bound I found a
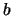
such that
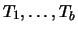
generate
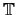
as a
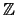
-module. I then
found a subset
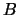
of the
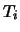
that form a
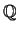
-basis for
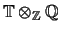
.
Next, viewing
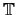
as a ring of matrices acting on
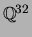
,
I found a random vector
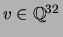
such that the set of
vectors
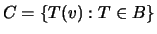
is linearly independent. Then
I wrote each of
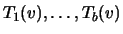
as
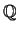
-linear combinations
of the elements of
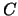
. Next I found a
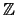
-basis
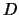
for the
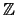
-span of these
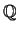
-linear combinations of elements of
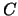
.
Tracing everything back, I find the trace pairing on
the elements of
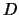
, and deduce the discriminant by computing
the determinant of the trace pairing matrix. The most difficult
step is computing
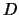
from
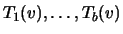
expressed
in terms of
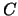
, and this explains why we embed
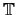
in
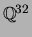
instead of viewing the elements of
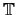
as vectors in
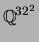
.
This whole computation takes one
second on an Athlon 2000 processor.
![]() the polynomial
the polynomial ![]() is congruent to
is congruent to