Let  be a global field. For each normalization
be a global field. For each normalization
 of
of  ,
let
,
let  denote the completion of
denote the completion of  . If
. If
 is
non-archimedean, let
is
non-archimedean, let  denote the ring of integers of
denote the ring of integers of  .
.
Definition 20.3.1 (Adele Ring)
The

of

is the topological ring whose
underlying topological space is the restricted topological product
of the

with respect to the

, and where addition and
multiplication are defined componentwise:
 for for  |
(20.4) |
It is readily verified that (i) this definition makes sense, i.e., if
 , then
, then
 and
and
 , whose components are
given by (20.3.1), are also in
, whose components are
given by (20.3.1), are also in  , and (ii) that
addition and multiplication are continuous in the
, and (ii) that
addition and multiplication are continuous in the  -topology, so
-topology, so
 is a topological ring, as asserted.
Also,
Lemma 20.2.4 implies that
is a topological ring, as asserted.
Also,
Lemma 20.2.4 implies that  is locally compact
because the
is locally compact
because the  are locally compact
(Corollary 17.1.6), and the
are locally compact
(Corollary 17.1.6), and the  are
compact (Theorem 17.1.4).
are
compact (Theorem 17.1.4).
There is a natural continuous ring inclusion
 |
(20.5) |
that sends 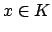 to the adele every one of whose components is
to the adele every one of whose components is  .
This is an adele because
.
This is an adele because
 for almost all
for almost all 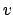 , by
Lemma 20.1.2. The map is injective because each map
, by
Lemma 20.1.2. The map is injective because each map  is an inclusion.
is an inclusion.
Definition 20.3.2 (Principal Adeles)
The image of (
20.3.2) is the ring of
.
It will cause no trouble to identify  with the principal adeles, so
we shall speak of
with the principal adeles, so
we shall speak of  as a subring of
as a subring of  .
.
Formation of the adeles is compatibility with base change, in the
following sense.
Lemma 20.3.3
Suppose  is a finite (separable) extension of the global field
is a finite (separable) extension of the global field
 . Then
. Then
 |
(20.6) |
both algebraically and topologically. Under this isomorphism,
maps isomorphically onto
 .
.
Proof.
Let

be a basis for

and let
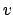
run through the normalized valuations
on

. The left hand side of (
20.3.3), with
the tensor product topology, is the restricted product of the
tensor products
with respect to the integers
 |
(20.7) |
(An element of the left hand side is a finite linear combination

of adeles

and coefficients

, and there is a natural isomorphism from the ring of such formal
sums to the restricted product of the

.)
We proved before (Theorem 19.1.8) that
where

are the normalizations of the extensions
of
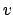
to

. Furthermore, as we proved using discriminants (see
Lemma
20.1.6), the above identification identifies
(
20.3.4) with
for almost all
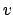
.
Thus the left hand side of (
20.3.3) is the restricted
product of the

with respect to the

.
But this is canonically isomorphic to the restricted product
of all completions

with respect to

, which
is the right hand side of (
20.3.3). This
establishes an isomorphism between the two sides of (
20.3.3)
as topological spaces. The map is also a ring homomorphism, so
the two sides are algebraically isomorphic, as claimed.

Proof.
For any nonzero

, the subgroup

of

is isomorphic as a topological group to
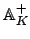
(the isomorphism is multiplication by

). By
Lemma
20.3.3, we have isomorphisms
If

, write

, with

.
Then
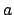
maps via the above map to
where

denotes the principal adele defined by

.
Under the final map,

maps to the tuple
The dimensions of

and of

over

are the same, so
this proves the final claim of the corollary.

Theorem 20.3.5
The global field  is discrete in
is discrete in  and the quotient
and the quotient
 of additive groups is compact in the quotient
topology.
of additive groups is compact in the quotient
topology.
At this point Cassels remarks
``It is impossible to conceive of any other uniquely
defined topology on  . This metamathematical reason is more
persuasive than the argument that follows!''
. This metamathematical reason is more
persuasive than the argument that follows!''
Proof.
Corollary
20.3.4, with

for

and

or

for

, shows that it is enough to verify
the theorem for

or

, and we shall do it
here for

.
To show that
 is discrete in
is discrete in
 it is enough, because of
the group structure, to find an open set
it is enough, because of
the group structure, to find an open set 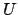 that contains
that contains
 , but which contains no other elements of
, but which contains no other elements of
 . (If
. (If
 , then
, then  is an open subset of
is an open subset of
 whose intersection with
whose intersection with
 is
is
 .)
We take for
.)
We take for 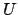 the set of
the set of
 with
with
where

and

are respectively the

-adic and the usual archimedean absolute values on

.
If

, then in the first place

because

for all

, and then

because

. This proves that

is discrete in

. (If we leave out one valuation,
as we will see later (Theorem
20.4.4), this theorem is
false--what goes wrong with the proof just given?)
Next we prove that the quotient
 is compact.
Let
is compact.
Let
 consist of the
consist of the
 with
with
We show that every adele

is of the form
which will imply that the compact set
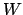
maps surjectively
onto

.
Fix an adele

. Since

is an adele, for each prime

we can find
a rational number
such that
and

almost all $p$

More precisely, for the finitely
many

such that
choose

to be a rational number that is the value of an appropriate truncation
of the

-adic expansion of

, and
when

just choose

.
Hence

is well defined.
The

for

do not mess up the inequality

since the
valuation

is non-archimedean and the

do not have any

in
their denominator:
Now choose

such that
Then

and

do what is required,
since

has the desired property
(since

and the

-adic valuations are
non-archimedean).
Hence the continuous map
 induced by the quotient
map
induced by the quotient
map
 is surjective. But
is surjective. But 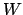 is compact
(being the topological product of the compact spaces
is compact
(being the topological product of the compact spaces
 and the
and the
 for all
for all  ), hence
), hence
 is also compact.
is also compact.

Proof.
We constructed such a set for

when proving
Theorem
20.3.5. For general

the
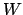
coming from the
proof determines compenent-wise a subset of

that is a subset of a set
with the properties claimed by the corollary.

As already remarked, 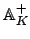 is a locally compact group, so it has
an invariant Haar measure. In fact one choice of this Haar measure is
the product of the Haar measures on the
is a locally compact group, so it has
an invariant Haar measure. In fact one choice of this Haar measure is
the product of the Haar measures on the  , in the sense
of Definition 20.2.5.
, in the sense
of Definition 20.2.5.
Corollary 20.3.7
The quotient
 has finite measure in the quotient measure
induced by the Haar measure on
has finite measure in the quotient measure
induced by the Haar measure on 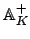 .
.
Remark 20.3.8
This statement is independent of the particular choice
of the multiplicative constant in the Haar measure
on
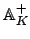
. We do not here go into the question of
finding the measure

in terms of our
explicitly given Haar measure. (See Tate's thesis,
[
Cp86, Chapter XV].)
Proof.
This can be reduced similarly to the case of

or

which is immediate, e.g., the
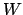
defined
above has measure
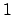
for our Haar measure.
Alternatively, finite measure follows from compactness. To see
this, cover
 with the translates of
with the translates of 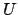 , where
, where 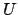 is a nonempty open
set with finite measure. The existence of a finite subcover implies
finite measure.
is a nonempty open
set with finite measure. The existence of a finite subcover implies
finite measure.

Remark 20.3.9
We give an alternative proof of the product formula

for nonzero

. We have seen that if

, then multiplication by

magnifies the Haar
measure in

by a factor of

. Hence if

, then multiplication by
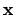
magnifies the
Haar measure in
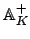
by

. But now
multiplication by

takes

into

, so
gives a well-defined bijection of

onto

which magnifies the measure by the factor

. Hence

Corollary
20.3.7. (The point is
that if

is the measure of

, then

, so because

is finite we must have

.)
William Stein
2004-05-06
. This metamathematical reason is more persuasive than the argument that follows!''
![]() is discrete in
is discrete in
![]() it is enough, because of
the group structure, to find an open set
it is enough, because of
the group structure, to find an open set ![]() that contains
that contains
![]() , but which contains no other elements of
, but which contains no other elements of
![]() . (If
. (If
![]() , then
, then ![]() is an open subset of
is an open subset of
![]() whose intersection with
whose intersection with
![]() is
is
![]() .)
We take for
.)
We take for ![]() the set of
the set of
![]() with
with
![]() is compact.
Let
is compact.
Let
![]() consist of the
consist of the
![]() with
with
 and
and


![]() induced by the quotient
map
induced by the quotient
map
![]() is surjective. But
is surjective. But ![]() is compact
(being the topological product of the compact spaces
is compact
(being the topological product of the compact spaces
![]() and the
and the
![]() for all
for all ![]() ), hence
), hence
![]() is also compact.
is also compact.
![]()
![]() is a locally compact group, so it has
an invariant Haar measure. In fact one choice of this Haar measure is
the product of the Haar measures on the
is a locally compact group, so it has
an invariant Haar measure. In fact one choice of this Haar measure is
the product of the Haar measures on the ![]() , in the sense
of Definition 20.2.5.
, in the sense
of Definition 20.2.5.
![]() with the translates of
with the translates of ![]() , where
, where ![]() is a nonempty open
set with finite measure. The existence of a finite subcover implies
finite measure.
is a nonempty open
set with finite measure. The existence of a finite subcover implies
finite measure.
![]()