We begin by finishing Dirichlet's proof that the group of units  of
of
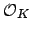 is isomorphic to
is isomorphic to
 , where
, where 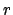 is the
number of real embeddings,
is the
number of real embeddings,  is half the number of complex
embeddings, and
is half the number of complex
embeddings, and  is the number of roots of unity in
is the number of roots of unity in  .
Recall that we defined a map
.
Recall that we defined a map
 by
Without much trouble, we proved that the kernel of
by
Without much trouble, we proved that the kernel of 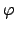 if finite
and the image
if finite
and the image 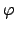 is discrete, and in the last section we
were finishing the proof that the image of
is discrete, and in the last section we
were finishing the proof that the image of 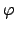 spans the subspace
spans the subspace
 of elements of
of elements of
 that are orthogonal to
that are orthogonal to
 , where
, where 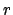 of the entries are
of the entries are 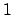 's and
's and  of them
are
of them
are 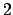 's. The somewhat
indirect route we followed was to suppose
i.e., that
's. The somewhat
indirect route we followed was to suppose
i.e., that 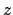 is not a multiple of
is not a multiple of 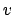 , and prove that
, and prove that 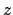 is not
orthogonal to some element of
is not
orthogonal to some element of
 . Writing
. Writing
 , this would show that
, this would show that
 , so
, so
 . We ran into two problems: (1) we ran out
of time, and (2) the notes contained an incomplete argument that a
quantity
. We ran into two problems: (1) we ran out
of time, and (2) the notes contained an incomplete argument that a
quantity
 can be chosen to be arbitrarily
large. We will finish going through a complete proof, then
compute many examples of unit groups using .
can be chosen to be arbitrarily
large. We will finish going through a complete proof, then
compute many examples of unit groups using .
Recall that
 was defined by
was defined by

(dot product)

and our goal is to show that there is a  such that
such that
 .
.
Our strategy is to use an appropriately chosen 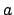 to construct a unit
to construct a unit
 such
such
 .
Recall that we used Blichfeld's lemma to find an
.
Recall that we used Blichfeld's lemma to find an
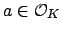 such that
such that
 ,
and
,
and
Let
 be
representative generators for the finitely many nonzero principal
ideals of
be
representative generators for the finitely many nonzero principal
ideals of 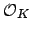 of norm at most
of norm at most
 . Modify the
. Modify the  to have the property
that
to have the property
that  is minimal among generators of
is minimal among generators of  (this is possible
because ideals are discrete). Note that the set
(this is possible
because ideals are discrete). Note that the set
 depends only on
depends only on  .
Since
.
Since
 , we have
, we have  , for some
, for some  , so there
is a unit
, so there
is a unit
 such that
such that  .
.
Let
Lemma 12.2.1
We have
and  depends only on
depends only on  and our fixed choice of
and our fixed choice of
 .
.
Proof.
By properties of logarithms,

. We next
use the triangle inequality

in various ways,
properties of logarithms, and the bounds (
12.2.1)
in the following computation:
The inequality of the lemma now follows.
That

only depends on

and our choice of
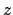
follows from the
formula for

and how we chose the

.

The amazing thing about Lemma 12.2.1 is that the bound  on
the right hand side does not depend on the
on
the right hand side does not depend on the  . Suppose we could
somehow cleverly choose the positive real numbers
. Suppose we could
somehow cleverly choose the positive real numbers  in such a way
that
in such a way
that

and

Then the facts that
 and
and  would together imply
that
would together imply
that  (since
(since  is closer to
is closer to  than
than  is to 0),
which is exactly what we aimed to prove. We finish the proof by
showing that it is possible to choose such
is to 0),
which is exactly what we aimed to prove. We finish the proof by
showing that it is possible to choose such  . Note that if we
change the
. Note that if we
change the  , then
, then 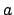 could change, hence the
could change, hence the  such that
such that
 is a unit could change, but the
is a unit could change, but the  don't change, just the
subscript
don't change, just the
subscript  . Also note that if
. Also note that if  , then we are trying to prove
that
, then we are trying to prove
that
 is a lattice in
is a lattice in
 , which is
automatically true, so we may assume that
, which is
automatically true, so we may assume that  .
.
Lemma 12.2.2
Assume  . Then
there is a choice of
. Then
there is a choice of
 such that
such that
Proof.
It is easier if we write
where

and

for

, and

and

for

,
The condition that
 is that the
is that the  are not all
the same, and in our new coordinates the lemma is equivalent to
showing that
are not all
the same, and in our new coordinates the lemma is equivalent to
showing that
 , subject to the
condition that
, subject to the
condition that
 . Order the
. Order the  so
that
so
that  . By hypothesis there exists a
. By hypothesis there exists a  such that
such that
 , and again re-ordering we may assume that
, and again re-ordering we may assume that  . Set
. Set
 . Then
. Then
 and
and  , so
, so
Since

, we have

as

.

William Stein
2004-05-06
![]() was defined by
was defined by
![]() to construct a unit
to construct a unit
![]() such
such
![]() .
Recall that we used Blichfeld's lemma to find an
.
Recall that we used Blichfeld's lemma to find an
![]() such that
such that
![]() ,
and
,
and
![]() be
representative generators for the finitely many nonzero principal
ideals of
be
representative generators for the finitely many nonzero principal
ideals of ![]() of norm at most
of norm at most
![]() . Modify the
. Modify the ![]() to have the property
that
to have the property
that ![]() is minimal among generators of
is minimal among generators of ![]() (this is possible
because ideals are discrete). Note that the set
(this is possible
because ideals are discrete). Note that the set
![]() depends only on
depends only on ![]() .
Since
.
Since
![]() , we have
, we have ![]() , for some
, for some ![]() , so there
is a unit
, so there
is a unit
![]() such that
such that ![]() .
.


![]() on
the right hand side does not depend on the
on
the right hand side does not depend on the ![]() . Suppose we could
somehow cleverly choose the positive real numbers
. Suppose we could
somehow cleverly choose the positive real numbers ![]() in such a way
that
in such a way
that

![]() is that the
is that the ![]() are not all
the same, and in our new coordinates the lemma is equivalent to
showing that
are not all
the same, and in our new coordinates the lemma is equivalent to
showing that
![]() , subject to the
condition that
, subject to the
condition that
![]() . Order the
. Order the ![]() so
that
so
that ![]() . By hypothesis there exists a
. By hypothesis there exists a ![]() such that
such that
![]() , and again re-ordering we may assume that
, and again re-ordering we may assume that ![]() . Set
. Set
![]() . Then
. Then
![]() and
and ![]() , so
, so
