We have seen examples in which 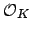 is not a unique factorization
domain. If
is not a unique factorization
domain. If 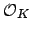 is a principal ideal domain, then it is a unique
factorization domain, so it is of interest to understand how badly
is a principal ideal domain, then it is a unique
factorization domain, so it is of interest to understand how badly
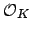 fails to be a principal ideal domain. The class group of
fails to be a principal ideal domain. The class group of
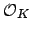 measures this failure. As one sees in a course on Class Field
Theory, the class group and its generalizations also yield deep
insight into the possible abelian Galois extensions of
measures this failure. As one sees in a course on Class Field
Theory, the class group and its generalizations also yield deep
insight into the possible abelian Galois extensions of  .
.
Definition 10.4.1 (Class Group)
Let
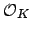
be the ring of integers of a number field

. The

of

is the group of nonzero fractional ideals
modulo the sugroup of principal fractional ideals

, for

.
Note that if we let  denote the group of nonzero fractional
ideals, then there is an exact sequence
denote the group of nonzero fractional
ideals, then there is an exact sequence
A basic theorem in algebraic number theory is that the class group
 is finite, which follows from the first part of the following
theorem and the fact that there are only finitely many ideals of norm
less than a given integer.
is finite, which follows from the first part of the following
theorem and the fact that there are only finitely many ideals of norm
less than a given integer.
The explicit bound in the theorem is called the Minkowski bound, and I think it
is the best known unconditional general bound (though there are better
bounds in certain special cases).
Before proving Theorem 10.4.2, we prove a few
lemmas. The strategy of the proof will be to start with any nonzero
ideal 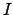 , and prove that there is some nonzero
, and prove that there is some nonzero  , with very
small norm, such that
, with very
small norm, such that  is an integral ideal. Then
is an integral ideal. Then
 will be small, since
will be small, since
 is small. The trick is to determine precisely
how small an
is small. The trick is to determine precisely
how small an 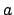 we can choose subject to the condition that
we can choose subject to the condition that
 be an integral ideal, i.e., that
be an integral ideal, i.e., that
 .
.
Let 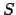 be a subset of
be a subset of
 . Then
. Then 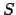 is
if whenever
is
if whenever  then the line connecting
then the line connecting  and
and  lies entirely in
lies entirely in 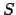 . We say that
. We say that 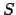 is if whenever
is if whenever  then
then  also.
If
also.
If  is a lattice in
is a lattice in  , then the of
, then the of  is
the volume of the compact real manifold
is
the volume of the compact real manifold  , which is the
same thing as the absolute value of the determinant of any
matrix whose rows form a basis for
, which is the
same thing as the absolute value of the determinant of any
matrix whose rows form a basis for  .
.
Proof.
Let

be an automorphism of

such that

. Then

defines an isomorphism of real manifolds

that changes
volume by a factor of
![$ \vert{\mathrm{Det}}(A)\vert=[L_1:L_2]$](img831.png)
. The claimed
formula then follows.

Fix a number field  with ring of integers
with ring of integers 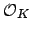 .
Let
.
Let
 be the embedding
be the embedding
where
 are the real embeddings
of
are the real embeddings
of  and
and
 are half
the complex embeddings of
are half
the complex embeddings of  , with one representative of
each pair of complex conjugate embeddings.
Note that this
, with one representative of
each pair of complex conjugate embeddings.
Note that this  is not exactly the same as the one
at the beginning of Section 10.2.
is not exactly the same as the one
at the beginning of Section 10.2.
Proof.
Let

.
From a basis

for
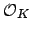
we obtain a matrix

whose
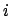
th row is
and whose determinant has absolute value equal to the volume
of

. By doing the following three column operations,
we obtain a matrix whose rows are exactly the images of
the

under
all embeddings of

into

, which
is the matrix that came up when we defined

.
- Add
 times each column with entries
Im
times each column with entries
Im to the column with entries
Re
to the column with entries
Re .
.
- Multiply all columns
Im
 by
by  , thus changing the determinant by
, thus changing the determinant by  .
.
- Add each columns with entries
Re
 to the the column with entries
to the the column with entries
 Im
Im .
.
Recalling the definition of discriminant, we see that if

is the matrix constructed by the above three
operations, then

.
Thus

Proof.
We know that
![$ [\O _K:I]=\Norm (I)$](img855.png)
is a nonzero rational number.
Lemma
10.4.5 implies that

is a lattice in

,
since

has rank
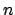
as abelian group and spans

,
so

is also a lattice in

. For the volume
formula, combine Lemmas
10.4.4-
10.4.5 to get

Proof.
[Proof of Theorem
10.4.2]
Let

be a number field with ring of integers
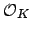
,
let

be as above,
and let

be the function defined by
Notice that if
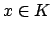
then
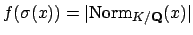
.
Let
 be any closed, bounded, convex, subset that is
symmetric with respect to the origin and has positive volume. Since
be any closed, bounded, convex, subset that is
symmetric with respect to the origin and has positive volume. Since  is closed
and bounded,
is closed
and bounded,
exists.
Suppose  is any nonzero fractional ideal of
is any nonzero fractional ideal of 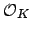 . Our goal
is to prove there is an integral ideal
. Our goal
is to prove there is an integral ideal  with small norm. We
will do this by finding an appropriate
with small norm. We
will do this by finding an appropriate
 .
By Lemma 10.4.6,
.
By Lemma 10.4.6,
Let

, where

.
Then
so by Lemma
10.4.3 there exists

.
Since

is the largest norm of an element of
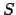
, the largest norm
of an element of

is at most

,
so
Since

, we have

, so

is an integral ideal of
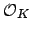
that is equivalent to
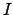
, and
Notice that the right hand side is independent of
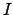
. It
depends only on
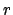
,

,

, and our choice of
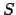
.
This completes the proof of the theorem, except for
the assertion that
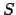
can be chosen to give the claim
at the end of the theorem, which we leave as an exercise.

Corollary 10.4.7
Suppose that
 is a number field. Then
is a number field. Then  .
.
Proof.
Applying Theorem
10.4.2 to the unit ideal,
we get the bound
Thus
and the right hand quantity is strictly bigger than
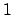
for
any

and any

(exercise).

Subsections
William Stein
2004-05-06
![]() denote the group of nonzero fractional
ideals, then there is an exact sequence
denote the group of nonzero fractional
ideals, then there is an exact sequence
![]() is finite, which follows from the first part of the following
theorem and the fact that there are only finitely many ideals of norm
less than a given integer.
is finite, which follows from the first part of the following
theorem and the fact that there are only finitely many ideals of norm
less than a given integer.

![]() , and prove that there is some nonzero
, and prove that there is some nonzero ![]() , with very
small norm, such that
, with very
small norm, such that ![]() is an integral ideal. Then
is an integral ideal. Then
![]() will be small, since
will be small, since
![]() is small. The trick is to determine precisely
how small an
is small. The trick is to determine precisely
how small an ![]() we can choose subject to the condition that
we can choose subject to the condition that
![]() be an integral ideal, i.e., that
be an integral ideal, i.e., that
![]() .
.
![]() be a subset of
be a subset of
![]() . Then
. Then ![]() is
if whenever
is
if whenever ![]() then the line connecting
then the line connecting ![]() and
and ![]() lies entirely in
lies entirely in ![]() . We say that
. We say that ![]() is if whenever
is if whenever ![]() then
then ![]() also.
If
also.
If ![]() is a lattice in
is a lattice in ![]() , then the of
, then the of ![]() is
the volume of the compact real manifold
is
the volume of the compact real manifold ![]() , which is the
same thing as the absolute value of the determinant of any
matrix whose rows form a basis for
, which is the
same thing as the absolute value of the determinant of any
matrix whose rows form a basis for ![]() .
.

![]() . Then for all
. Then for all
![]() there is
there is
![]() ,
since
,
since
![]() .
If
.
If
![]() then the
then the
![]() are all in
are all in
![]() ,
which is finite since
,
which is finite since ![]() is bounded and
is bounded and ![]() is discrete.
Hence there exists
is discrete.
Hence there exists
![]() for arbitrarily
small
for arbitrarily
small
![]() . Since
. Since ![]() is closed,
is closed,
![]() .
.
![]()
![]() with ring of integers
with ring of integers ![]() .
Let
.
Let
![]() be the embedding
be the embedding
![]() be any closed, bounded, convex, subset that is
symmetric with respect to the origin and has positive volume. Since
be any closed, bounded, convex, subset that is
symmetric with respect to the origin and has positive volume. Since ![]() is closed
and bounded,
is closed
and bounded,
![]() is any nonzero fractional ideal of
is any nonzero fractional ideal of ![]() . Our goal
is to prove there is an integral ideal
. Our goal
is to prove there is an integral ideal ![]() with small norm. We
will do this by finding an appropriate
with small norm. We
will do this by finding an appropriate
![]() .
By Lemma 10.4.6,
.
By Lemma 10.4.6,


