



Next: -adic Heights
Up: Non-classical Modular Forms
Previous: Hilbert-Siegel Modular Forms
Contents
(Written by Paul Gunnells.)
Here are some problems, both computational and theoretical, about
computing with cohomology of arithmetic groups in
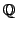 -rank
-rank 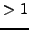 .
Many of these are discussed in more detail in the appendix to the
book [Ste07]. I thank Avner Ash for suggesting problems (2)
and (3), and for many helpful discussions.
.
Many of these are discussed in more detail in the appendix to the
book [Ste07]. I thank Avner Ash for suggesting problems (2)
and (3), and for many helpful discussions.
Problem 5.2.1
- Implement a robust user-friendly program to explore
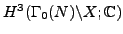 , where
, where
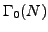 is a
congruence subgroup of
is a
congruence subgroup of
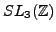 , and
, and 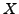 is the symmetric space
is the symmetric space
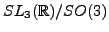 . In particular your program should be able to
compute a basis for the cohomology space and compute the action of
the Hecke operators. One public version of such a program exists on
the net at the homepage of Wilberd van der Kallen, but it's in
Pascal and isn't maintained. Nevertheless it might be a good
starting point.
. In particular your program should be able to
compute a basis for the cohomology space and compute the action of
the Hecke operators. One public version of such a program exists on
the net at the homepage of Wilberd van der Kallen, but it's in
Pascal and isn't maintained. Nevertheless it might be a good
starting point.
- Beef up your program to include local coefficient systems.
- Beef it up even more to include integral and torsion coefficients.
- Distribute your tool to the world by incorporating
it into SAGE [SJ05].
Problem 5.2.2
- Let
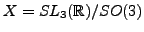 and let
and let
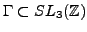 be a congruence subgroup. Investigate the cohomology of the boundary
of the Borel-Serre compactification of
be a congruence subgroup. Investigate the cohomology of the boundary
of the Borel-Serre compactification of
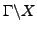 with
coefficients
with
coefficients
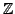 or
or
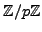 .
.
- Use the algorithm in [Gun00] to compute the Hecke
action on
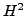 of the boundary.
of the boundary.
- Extend these computations to other
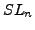 s.
s.
Problem 5.2.5
- Extend the algorithm of [Gun00] to the cohomology of
subgroups of
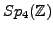 .
.
- (G.Harder [Har]) Use your algorithm to
investigate congruences between Siegel modular forms and elliptic
modular forms.
Problem 5.2.6
- Investigate the connections between the different notions of
perfect quadratic forms in the literature (cf. [Ste07, A.6.2]).
- Can the computational data from the work of
Baeza-Coulangeon-Icaza-O'Ryan [BCIO01] be used to construct
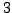 (real) dimensional deformation retracts of Hilbert modular varieties
that can be used to compute cohomology?
(real) dimensional deformation retracts of Hilbert modular varieties
that can be used to compute cohomology?
- If not deformation retracts,
can you use the data to construct cell complexes with actions of Hilbert modular
groups that can then be used to compute cohomology?
Problem 5.2.7
Study the Vorono
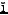
polyhedron for complex quadratic fields
for
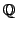
-ranks
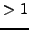
(cf. [
Sta79]).
Problem 5.2.8
- Study the geometry and combinatorics of the retract for
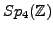 [MM93,MM89]. Use the retract to compute cohomology of subgroups
of
[MM93,MM89]. Use the retract to compute cohomology of subgroups
of
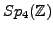 with various coefficients.
with various coefficients.
- Can you characterize the sets of vectors that parameterize
cells in the retract, analogous to Vorono
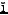 's characterization for
the
's characterization for
the
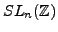 retract?
retract?
- Can you define a retract for
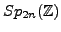 ?
?




Next: -adic Heights
Up: Non-classical Modular Forms
Previous: Hilbert-Siegel Modular Forms
Contents
William Stein
2006-10-20
![]() -rank
-rank ![]() .
Many of these are discussed in more detail in the appendix to the
book [Ste07]. I thank Avner Ash for suggesting problems (2)
and (3), and for many helpful discussions.
.
Many of these are discussed in more detail in the appendix to the
book [Ste07]. I thank Avner Ash for suggesting problems (2)
and (3), and for many helpful discussions.