



Next: About this document ...
Up: MSRI Modular Forms Summer
Previous: Other Projects
Contents
- AGM02
-
Avner Ash, Paul E. Gunnells, and Mark McConnell, Cohomology of congruence
subgroups of
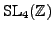 , J. Number Theory 94 (2002),
no. 1, 181-212.
, J. Number Theory 94 (2002),
no. 1, 181-212.
- ARS06
-
A. Agashe, K.A. Ribet, and W.A. Stein, The
Manin Constant, JPAM Coates Volume (2006),
http://modular.math.washington.edu/papers/ars-manin/.
- AS05
-
A. Agashe and W. Stein, Visible evidence for the Birch and
Swinnerton-Dyer conjecture for modular abelian varieties of analytic rank
zero, Math. Comp. 74 (2005), no. 249, 455-484 (electronic), With
an appendix by J. Cremona and B. Mazur.
- Ash92
-
Avner Ash, Galois representations attached to mod
 cohomology of
cohomology of
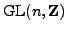 , Duke Math. J. 65 (1992), no. 2, 235-255.
, Duke Math. J. 65 (1992), no. 2, 235-255.
- BCIO01
-
Ricardo Baeza, Renaud Coulangeon, Maria Ines Icaza, and Manuel O'Ryan,
Hermite's constant for quadratic number fields, Experiment. Math.
10 (2001), no. 4, 543-551.
- Bes04
-
Amnon Besser, The
 -adic height pairings of Coleman-Gross and of
Nekovár, Number theory, CRM Proc. Lecture Notes, vol. 36, Amer. Math.
Soc., Providence, RI, 2004, pp. 13-25.
-adic height pairings of Coleman-Gross and of
Nekovár, Number theory, CRM Proc. Lecture Notes, vol. 36, Amer. Math.
Soc., Providence, RI, 2004, pp. 13-25.
- CF99
-
J.B. Conrey and D.W. Farmer, Hecke operators and
the nonvanishing of
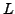 -functions, Topics in number theory (University
Park, PA, 1997), Math. Appl., vol. 467, Kluwer Acad. Publ., Dordrecht, 1999,
pp. 143-150.
-functions, Topics in number theory (University
Park, PA, 1997), Math. Appl., vol. 467, Kluwer Acad. Publ., Dordrecht, 1999,
pp. 143-150.
- Col91
-
Robert F. Coleman, The universal vectorial bi-extension and
 -adic
heights, Invent. Math. 103 (1991), no. 3, 631-650.
-adic
heights, Invent. Math. 103 (1991), no. 3, 631-650.
- Col03
-
R. Coleman, Approximation of infinite-slope modular eigenforms by
finite-slope eigenforms, to appear in the Dwork Proceedings (2003).
- CS01
-
B. Conrad and W.A. Stein, Component groups of purely toric
quotients, Math. Res. Lett. 8 (2001), no. 5-6, 745-766.
- Dia95
-
F. Diamond, The refined conjecture of Serre, Elliptic curves,
modular forms, & Fermat's last theorem (Hong
Kong, 1993) (Cambridge, MA), Internat. Press, 1995, pp. 22-37.
- Edi
-
B. Edixhoven, Point counting after Kedlaya, EIDMA-Stieltjes
graduate course, Leiden, September 22-26,2003,
http://www.math.leidenuniv.nl/ edix/oww/mathofcrypt/carls_edixhoven/kedlaya.pdf.
- FJ02
-
D. W. Farmer and K. James, The irreducibility of some level 1 Hecke
polynomials, Math. Comp. 71 (2002), no. 239, 1263-1270
(electronic).
- GL01
-
Josep González and Joan-C. Lario,
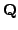 -curves and their
Manin ideals, Amer. J. Math. 123 (2001), no. 3, 475-503.
-curves and their
Manin ideals, Amer. J. Math. 123 (2001), no. 3, 475-503.
- Gun00
-
P. E. Gunnells, Computing Hecke eigenvalues below the cohomological
dimension, Experiment. Math. 9 (2000), no. 3, 351-367.
- Har
-
G. Harder, Congruences between modular forms of genus 1 and of genus 2,
Arbeitstagung.
- IW03
-
Adrian Iovita and Annette Werner,
 -adic height pairings on abelian
varieties with semistable ordinary reduction, J. Reine Angew. Math.
564 (2003), 181-203.
-adic height pairings on abelian
varieties with semistable ordinary reduction, J. Reine Angew. Math.
564 (2003), 181-203.
- Ked01
-
Kiran S. Kedlaya, Counting points on hyperelliptic curves using
Monsky-Washnitzer cohomology, J. Ramanujan Math. Soc. 16
(2001), no. 4, 323-338.
- Ked04
-
K. Kedlaya, Computing zeta functions via
 -adic cohomology,
Algorithmic number theory, Lecture Notes in Comput. Sci., vol. 3076,
Springer, Berlin, 2004, pp. 1-17.
-adic cohomology,
Algorithmic number theory, Lecture Notes in Comput. Sci., vol. 3076,
Springer, Berlin, 2004, pp. 1-17.
- KS00
-
D.R. Kohel and W.A. Stein, Component Groups of
Quotients of
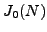 , Proceedings of the 4th International
Symposium (ANTS-IV), Leiden, Netherlands, July 2-7, 2000 (Berlin), Springer,
2000.
, Proceedings of the 4th International
Symposium (ANTS-IV), Leiden, Netherlands, July 2-7, 2000 (Berlin), Springer,
2000.
- MM89
-
R. MacPherson and M. McConnell, Classical projective geometry and modular
varieties, Algebraic analysis, geometry, and number theory (Baltimore, MD,
1988), Johns Hopkins Univ. Press, Baltimore, MD, 1989, pp. 237-290.
- MM93
-
to3em, Explicit reduction theory for Siegel modular threefolds,
Invent. Math. 111 (1993), no. 3, 575-625.
- MST06
-
B. Mazur, W. Stein, and J. Tate, Computation of
 -adic heights and log
convergence, To appear in Documenta Mathematica's Coates Volume.
-adic heights and log
convergence, To appear in Documenta Mathematica's Coates Volume.
- MT83
-
B. Mazur and J. Tate, Canonical height pairings via biextensions,
Arithmetic and geometry, Vol. I, Progr. Math., vol. 35, Birkhäuser Boston,
Boston, MA, 1983, pp. 195-237.
- MT87
-
to3em, Refined conjectures of the ``Birch and Swinnerton-Dyer
type'', Duke Math. J. 54 (1987), no. 2, 711-750.
- MT91
-
to3em, The
 -adic sigma function, Duke Math. J. 62
(1991), no. 3, 663-688.
-adic sigma function, Duke Math. J. 62
(1991), no. 3, 663-688.
- Nek93
-
Jan Nekovár, On
 -adic height pairings, Séminaire de
Théorie des Nombres, Paris, 1990-91, Progr. Math., vol. 108, Birkhäuser
Boston, Boston, MA, 1993, pp. 127-202.
-adic height pairings, Séminaire de
Théorie des Nombres, Paris, 1990-91, Progr. Math., vol. 108, Birkhäuser
Boston, Boston, MA, 1993, pp. 127-202.
- Pla94
-
Andrew Plater, Supersingular
 -adic height pairings on elliptic
curves, Arithmetic geometry (Tempe, AZ, 1993), Contemp. Math., vol. 174,
Amer. Math. Soc., Providence, RI, 1994, pp. 95-105.
-adic height pairings on elliptic
curves, Arithmetic geometry (Tempe, AZ, 1993), Contemp. Math., vol. 174,
Amer. Math. Soc., Providence, RI, 1994, pp. 95-105.
- PR03
-
Bernadette Perrin-Riou, Arithmétique des courbes elliptiques à
réduction supersingulière en
 , Experiment. Math. 12
(2003), no. 2, 155-186.
, Experiment. Math. 12
(2003), no. 2, 155-186.
- Rib92
-
K.A. Ribet, Abelian varieties over
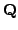 and modular
forms, Algebra and topology 1992 (Taejon), Korea Adv. Inst. Sci. Tech.,
Taejon, 1992, pp. 53-79.
and modular
forms, Algebra and topology 1992 (Taejon), Korea Adv. Inst. Sci. Tech.,
Taejon, 1992, pp. 53-79.
- RS01
-
K.A. Ribet and W.A. Stein, Lectures on Serre's
conjectures, Arithmetic algebraic geometry (Park City, UT, 1999), IAS/Park
City Math. Ser., vol. 9, Amer. Math. Soc., Providence, RI, 2001,
pp. 143-232.
- Sch82
-
Peter Schneider,
 -adic height pairings. I, Invent. Math.
69 (1982), no. 3, 401-409.
-adic height pairings. I, Invent. Math.
69 (1982), no. 3, 401-409.
- Sch85
-
to3em,
 -adic height pairings. II, Invent. Math. 79
(1985), no. 2, 329-374.
-adic height pairings. II, Invent. Math. 79
(1985), no. 2, 329-374.
- SJ05
-
W. Stein and D. Joyner, Sage: System for algebra and geometry
experimentation, Communications in Computer Algebra (SIGSAM Bulletin)
39 (June 2005), no. 2, http://sage.sourceforge.net/.
- Sta79
-
R. E. Staffeldt, Reduction theory and
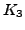 of the Gaussian
integers, Duke Math. J. 46 (1979), no. 4, 773-798.
of the Gaussian
integers, Duke Math. J. 46 (1979), no. 4, 773-798.
- Ste89
-
G. Stevens, Stickelberger elements and modular parametrizations of
elliptic curves, Invent. Math. 98 (1989), no. 1, 75-106.
- Ste07
-
W. Stein, Explicitly computing with modular forms, Graduate Studies in
Mathematics, American Math Society, 2007.
- SW04
-
W. Stein and M. Watkins, Modular parametrizations of Neumann-Setzer
elliptic curves, Int. Math. Res. Not. (2004), no. 27, 1395-1405.
- Zar90
-
Yuri G. Zarhin,
 -adic heights on abelian varieties, Séminaire de
Théorie des Nombres, Paris 1987-88, Progr. Math., vol. 81, Birkhäuser
Boston, Boston, MA, 1990, pp. 317-341.
-adic heights on abelian varieties, Séminaire de
Théorie des Nombres, Paris 1987-88, Progr. Math., vol. 81, Birkhäuser
Boston, Boston, MA, 1990, pp. 317-341.
William Stein
2006-10-20