Let ![]() be an odd prime number, and
be an odd prime number, and ![]() an elliptic curve over a
global field
an elliptic curve over a
global field ![]() that has good ordinary reduction at
that has good ordinary reduction at ![]() . Let
. Let ![]() be
any (infinite degree) Galois extension with a continuous injective
homomorphism
be
any (infinite degree) Galois extension with a continuous injective
homomorphism ![]() of its Galois group to
of its Galois group to
![]() . To the data
. To the data
![]() , one associates6.1 a canonical (bilinear, symmetric)
(
, one associates6.1 a canonical (bilinear, symmetric)
(![]() -adic) height pairing
-adic) height pairing
Such pairings are of great interest for the arithmetic of
The goal of this project is to investigate some computational
questions regarding ![]() -adic height pairings. The main stumbling
block to computing them efficiently is in calculating, for each of the
completions
-adic height pairings. The main stumbling
block to computing them efficiently is in calculating, for each of the
completions ![]() at the places
at the places ![]() of
of ![]() dividing
dividing ![]() , the value of
the
, the value of
the ![]() -adic modular form
-adic modular form ![]() associated to the elliptic curve
with a chosen Weierstrass form of good reduction over
associated to the elliptic curve
with a chosen Weierstrass form of good reduction over ![]() .
.
The paper [MST06] contains an algorithm for
computing these quantities (for
![]() ), i.e., for computing the value
of
), i.e., for computing the value
of ![]() of an elliptic curve (that builds on the works of Katz
and Kedlaya listed in our bibliography).
of an elliptic curve (that builds on the works of Katz
and Kedlaya listed in our bibliography).
The paper [MST06] also discusses the ![]() -adic
convergence rate of canonical expansions of the
-adic
convergence rate of canonical expansions of the ![]() -adic modular form
-adic modular form
![]() on the Hasse domain, where for
on the Hasse domain, where for ![]() we view
we view ![]() as an infinite sum of classical modular forms divided by
powers of the (classical) modular form
as an infinite sum of classical modular forms divided by
powers of the (classical) modular form
![]() , while for
, while for
![]() we view it as a sum of classical modular forms divided by
powers of
we view it as a sum of classical modular forms divided by
powers of ![]() .
.
We were led to our fast method of computing
![]() by our realization
that the more naive methods, of computing it by integrality or by
approximations to it as function on the Hasse domain, were not
practical, because the convergence is ``logarithmic'' in the sense
that the
by our realization
that the more naive methods, of computing it by integrality or by
approximations to it as function on the Hasse domain, were not
practical, because the convergence is ``logarithmic'' in the sense
that the ![]() th convergent gives only an accuracy of
th convergent gives only an accuracy of ![]() .
.
The reason why this constant ![]() enters the calculation is
because it is needed for the computation of the
enters the calculation is
because it is needed for the computation of the ![]() -adic sigma
function [MT91], which in turn is the critical
element in the formulas for height pairings.
-adic sigma
function [MT91], which in turn is the critical
element in the formulas for height pairings.
For example, let us consider the cyclotomic ![]() -adic height
pairing in the special case where
-adic height
pairing in the special case where
![]() and
and ![]() .
.
If
![]() is the Galois group of an algebraic closure of
is the Galois group of an algebraic closure of
![]() over
over
![]() , we have the natural surjective continuous homomorphism
, we have the natural surjective continuous homomorphism
![]() pinned down by the standard formula
pinned down by the standard formula
![]() where
where
![]() and
and ![]() is any
is any ![]() -power
root of unity. The
-power
root of unity. The ![]() -adic logarithm
-adic logarithm
![]() is
the unique group homomorphism with
is
the unique group homomorphism with
![]() that extends the
homomorphism
that extends the
homomorphism
![]() defined by the usual power
series of
defined by the usual power
series of ![]() about
about ![]() . Explicitly, if
. Explicitly, if
![]() , then
, then
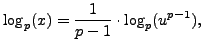
where
The composition
![]() is a cyclotomic
linear functional
is a cyclotomic
linear functional
![]() which, in the body of our text,
will be dealt with (thanks to class field theory) as the idele class
functional that we denote
which, in the body of our text,
will be dealt with (thanks to class field theory) as the idele class
functional that we denote
![]() .
.
Let
![]() denote the Néron model of
denote the Néron model of ![]() over
over
![]() . Let
. Let
![]() be a non-torsion point that reduces to
be a non-torsion point that reduces to
![]() and to the
connected component of
and to the
connected component of
![]() at all primes
at all primes ![]() of bad
reduction for
of bad
reduction for ![]() . Because
. Because
![]() is a unique factorization domain, any
nonzero point
is a unique factorization domain, any
nonzero point
![]() can be written uniquely in the
form
can be written uniquely in the
form
![]() , where
, where
![]() ,
,
![]() ,
and
,
and ![]() . The function
. The function ![]() assigns to
assigns to ![]() this square root
this square root ![]() of
the denominator of
of
the denominator of ![]() .
.
Here is the formula for the cyclotomic ![]() -adic height of
-adic height of ![]() ,
i.e., the value of
,
i.e., the value of
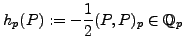
where
Here
![]() is the
is the ![]() -adic sigma function of
[MT91] associated to the pair
-adic sigma function of
[MT91] associated to the pair
![]() .
The
.
The ![]() -function depends only on
-function depends only on
![]() and not on a choice of
Weierstrass equation, and behaves like a modular form of weight
and not on a choice of
Weierstrass equation, and behaves like a modular form of weight ![]() , that
is
, that
is
![]() . It is ``quadratic''
the sense that for any
. It is ``quadratic''
the sense that for any
![]() and point
and point ![]() in the
formal group
in the
formal group
![]() ,
we have
,
we have
The height function ![]() of (6.1.1) extends uniquely to
a function on the full Mordell-Weil group
of (6.1.1) extends uniquely to
a function on the full Mordell-Weil group
![]() that satisfies
that satisfies
![]() for all integers
for all integers ![]() and
and
![]() . For
. For
![]() , setting
, setting
we obtain a pairing on
The ![]() -adic
-adic ![]() function is the most mysterious quantity in
(6.1.1).
There are many ways to define
function is the most mysterious quantity in
(6.1.1).
There are many ways to define ![]() , e.g., [MT91]
contains
, e.g., [MT91]
contains ![]() different characterizations of
different characterizations of ![]() ! We now
describe a characterization that leads directly to a (slow!) algorithm
to compute
! We now
describe a characterization that leads directly to a (slow!) algorithm
to compute ![]() . Let
. Let
In (6.1.1),
by ![]() we mean
we mean
![]() , where
, where ![]() . We have thus
given a complete definition of
. We have thus
given a complete definition of ![]() for any point
for any point
![]() and a prime
and a prime ![]() of good ordinary reduction for
of good ordinary reduction for ![]() .
.