



Next: Level Raising and Lowering
Up: An Example: Computing
Previous: Source Code
Contents
There remain many exciting problems to consider in the computation of 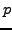 -adic heights for elliptic curves. Below we outline a few:
-adic heights for elliptic curves. Below we outline a few:
Problem 6.2.4
Are there simplifications one could make to the above
algorithm taking into account the fact that we're working with
elliptic curves (e.g., using group structure, etc.)? Should we
expect that the matrix of Frobenius be easier to compute in the
case of genus 1 curves?
Problem 6.2.5
A question of John Tate: how does
the cyclotomic
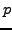
-adic height pairing change for families of
elliptic curves, e.g.,
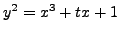
? What about considering
families with constant
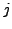
-invariant? Non-constant
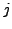
-invariant?
Curves with complex multiplication? Curves without complex
multiplication?
Remark 6.2.6 (From Christian Wuthrich)
In my J. London Soc. article I computed
some and proved that they are locally analytic. The height of a
section can have zeroes as a rigid
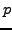
-adic analytic function. If
the conjecture on the non-degeneracy of the heights is true, then
the zeroes are not in
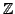
but in
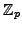
. But I have no
interpretation of what they could mean.
Problem 6.2.7
Extend the above algorithm to implement the computation of
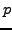
-adic
anticyclotomic heights, using new ideas of Mazur in
[
MST06].
Problem 6.2.8 (From Christian Wuthrich.)
For computational reasons it would be
interesting to also include the primes
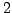
and
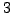
. It should be
possible to write a more complicated Kedlaya algorithm at least for
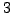
. In shark I reprogrammed the original approximation algorithm
(beware
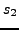
is not exactly integral) for
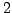
and
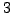
so that I can
compute
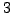
-primary parts of Sha. Kato's theorem is not known to me
for
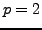
.
Problem 6.2.9 (From Christian Wuthrich.)
There is a well-defined supersingular
theory explained by Perrin-Riou. The Kedlaya algorithm can be used
to compute the
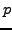
-adic heights also in this case. As I did it in
shark. In shark there are also
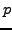
-adic heights for multiplicative
primes using Mazur-Tate-Teitelbaum. Additive primes are a bit
harder, one needs to pass to an extension over which they become
semi-stable. So this calls for
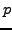
-adic height over arbitrary number
fields.




Next: Level Raising and Lowering
Up: An Example: Computing
Previous: Source Code
Contents
William Stein
2006-10-20