Suppose
Write
We call
the 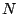 th degree Taylor polynomial.
Notice that
if and only if
We would like to estimate
th degree Taylor polynomial.
Notice that
if and only if
We would like to estimate 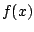 with
with 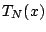 . We need
an estimate for
. We need
an estimate for 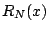 .
.
Theorem 6.7.1 (Taylor's theorem)
If
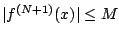 for
for
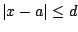 , then
, then
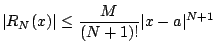
for $|x-a|&le#leq;d$.
For example, if 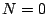 , this says that
i.e.,
which should look familiar from a previous class (Mean Value Theorem).
, this says that
i.e.,
which should look familiar from a previous class (Mean Value Theorem).
Applications:
- One can use Theorem
![[*]](/usr/share/latex2html/icons/crossref.png) to
prove that functions converge to their Taylor series.
to
prove that functions converge to their Taylor series.
- Returning to the relativity example above, we apply Taylor's theorem
with
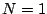 and
and 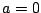 . With
. With
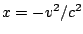 and
and 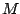 any number such
that
any number such
that
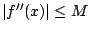 , we have
For example, if we assume that
, we have
For example, if we assume that
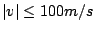 we use
we use
Using
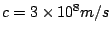 , we get
, we get
Thus for
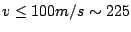 mph, then the error in throwing away
relativistic factors is
mph, then the error in throwing away
relativistic factors is
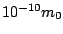 . This is like 200 feet out of
the distance to the sun (93 million miles).
So relativistic and Newtonian kinetic energies are almost the same
for reasonable speeds.
. This is like 200 feet out of
the distance to the sun (93 million miles).
So relativistic and Newtonian kinetic energies are almost the same
for reasonable speeds.
William Stein
2006-03-15
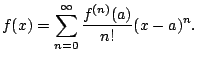
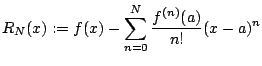
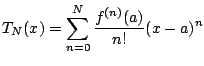
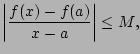
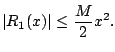
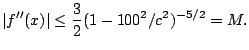
![]() , we get
, we get