Next: Estimation of Taylor Series Up: Sequences and Series Previous: Taylor Series Contents Index
| Final exam: Wednesday, March 22, 7-10pm in PCYNH 109. Bring ID!
Last Quiz 4: Today (last one) Today: 11.12 Applications of Taylor Polynomials Next; Differential Equations |
This section is about an example in the theory of relativity. Let ![]() be the (relativistic) mass of an object and
be the (relativistic) mass of an object and ![]() be the mass at rest
(rest mass) of the object. Let
be the mass at rest
(rest mass) of the object. Let ![]() be the velocity of the object relative to the
observer, and let
be the velocity of the object relative to the
observer, and let ![]() be the speed of light. These three quantities
are related as follows:
be the speed of light. These three quantities
are related as follows:
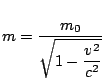 (relativistic) mass
(relativistic) mass
Notice that
![$\displaystyle mc^2 - m_0 c^2 = \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} - m_0 c^2
= m_0 c^2 \left[ \left(1 - \frac{v^2}{c^2}\right)^{-\frac{1}{2}} - 1\right].
$](img1297.png)
Let's compute the Taylor series of ![]() . We have
. We have
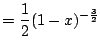 |
||
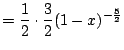 |
||
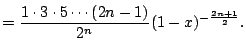 |
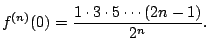
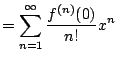 |
||
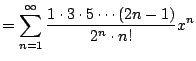 |
||
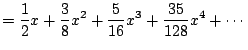 |
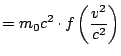 |
||
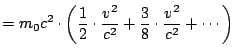 |
||
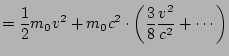 |
And we can ignore the higher order terms if
![]() is small.
But how small is ``small'' enough, given that
is small.
But how small is ``small'' enough, given that
![]() appears
in an infinite sum?
appears
in an infinite sum?