Next: Computing Volumes of Surfaces Up: Using Integration to Determine Previous: Using Integration to Determine Contents Index
![$\displaystyle = \int_{-1}^2 \Bigl[(9-x^2) - (x+1)\Bigr] dx
$](img187.png)
![$\displaystyle \int_{-1}^2 [(9-x^2) - (x+1)] dx
= \int_{-1}^2 (8-x-x^2)dx
= \left[ 8x - \frac{1}{2}x^2 - \frac{1}{3}x^3 \right]_{-1}^2
= \frac{39}{2}.
$](img188.png)
The above example illustrates the simplest case. In practice
more interesting situations often arise.
The next example illustrates finding the boundary points ![]() when they are not explicitly given.
when they are not explicitly given.
Problem: We didn't tell you what the boundary points ![]() are. We have to figure that out. How? We must find
exactly where the two curves intersect, by setting
the two curves equal and finding the solution.
We have
are. We have to figure that out. How? We must find
exactly where the two curves intersect, by setting
the two curves equal and finding the solution.
We have
![$\displaystyle \int_{-3}^3 \left[12-x^2 - (x^2-6)\right] dx
= \int_{-3}^3 (18 - 2x^2) dx
= 4 \int_{0}^3 (9 - x^2) dx
= 4 \cdot 18 = 72.
$](img196.png)
Write
![]() , so that we can obtain
the graph of the parabola by shifting the standard graph.
The area comes in two pieces, and the upper and lower curve switch in
the middle.
Technically, what we're doing is integrating the
absolute value of the difference.
The area is
, so that we can obtain
the graph of the parabola by shifting the standard graph.
The area comes in two pieces, and the upper and lower curve switch in
the middle.
Technically, what we're doing is integrating the
absolute value of the difference.
The area is
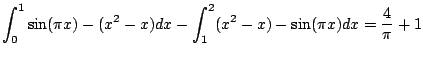
Something to take away from this is that in order to solve this sort of problem, you need some facility with graphing functions. If you aren't comfortable with this, review.
William Stein 2006-03-15