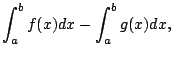Next: Examples Up: Applications to Areas, Volume, Previous: Applications to Areas, Volume, Contents Index
| Today is 2006-01-18.
Quiz reminder: Friday, Jan 20 (describe format) How was your weekend? Mine was great--I wrote open source math software nonstop for days on end! |
This section is about how to compute the area of fairly general regions in the plane. Regions are often described as the area enclosed by the graphs of several curves. (``My land is the plot enclosed by that river, that fence, and the highway.'')
Recall that the integral
![]() has a geometric
interpretation as the signed area between the graph of
has a geometric
interpretation as the signed area between the graph of ![]() and the
and the
![]() -axis. We defined area by subdividing, adding up approximate areas
(use points in the intervals) as Riemann sum, and taking the limit.
Thus we defined area as a limit of Riemann sums. The fundamental
theorem of calculus asserts that we can compute areas exactly when
we can finding antiderivatives.
-axis. We defined area by subdividing, adding up approximate areas
(use points in the intervals) as Riemann sum, and taking the limit.
Thus we defined area as a limit of Riemann sums. The fundamental
theorem of calculus asserts that we can compute areas exactly when
we can finding antiderivatives.
Instead of considering the area between the graph of ![]() and the
and the ![]() -axis, we consider more generally two graphs,
-axis, we consider more generally two graphs,
![]() ,
, ![]() , and assume for simplicity that
, and assume for simplicity that
![]() on an interval
on an interval ![]() .
Again, we approximate the area between these two
curves as before using Riemann sums.
Each approximating rectangle has width
.
Again, we approximate the area between these two
curves as before using Riemann sums.
Each approximating rectangle has width ![]() and height
and height
![]() , so
, so
Why did we make a big deal about approximations instead of just writing down (3.1.1)? Because having a sense of how this area comes directly from a Riemann sum is very important. But, what is the point of the Riemann sum if all we're going to do is write down the integral? The sum embodies the geometric manifestation of the integral. If you have this picture in your mind, then the Riemann sum has done its job. If you understand this, you're more likely to know what integral to write down; if you don't, then you might not.