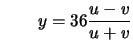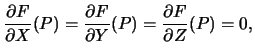Next: Motivation: The Congruent Number
Up: New reading and problems
Previous: New reading and problems
- (Jeff)
Let
 be the set of triples
be the set of triples
![$ [a,b,c]$](img51.png) modulo scalar multiplication,
as usual. Define a line in
modulo scalar multiplication,
as usual. Define a line in  to be the set
of solutions of an equation of the form
for some numbers
to be the set
of solutions of an equation of the form
for some numbers 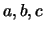 not all zero.
Prove (from the definition) that any two distinct points in
not all zero.
Prove (from the definition) that any two distinct points in
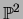 are contained in a unique line.
Then prove that any two distinct lines in
are contained in a unique line.
Then prove that any two distinct lines in 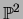 intersect
in a unique point.
intersect
in a unique point.
- (Jennifer)
Let
![$ F(X,Y,Z) \in {\mathbb{C}}[X,Y,Z]$](img54.png) be a homogeneous polynomial
of degree
be a homogeneous polynomial
of degree 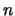 . Prove that the partial derivatives of
. Prove that the partial derivatives of 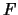 are homogeneous polynomials of degree
are homogeneous polynomials of degree 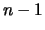 , and use
this to show that
by differentiating
, and use
this to show that
by differentiating
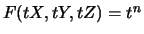 with respect
to
with respect
to 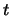 .
.
- (Mauro)
- Let
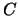 be a curve in
be a curve in 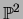 defined by
defined by
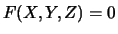 ,
where
,
where 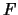 is a homogenous polynomial.
Prove that if
is a homogenous polynomial.
Prove that if
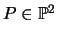 satifies the equation
satifies the equation
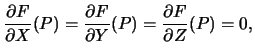 |
(1) |
then 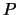 ``automatically'' satisfies
``automatically'' satisfies 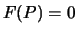 .
Thus to find the singular points on
.
Thus to find the singular points on 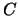 , you just
have to find the common solutions to (1);
it is not necessary to include
, you just
have to find the common solutions to (1);
it is not necessary to include 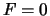 .
.
- Find all singular points on the curve
defined by
- (Alex)
For each of the given affine curves
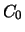 , find a projective
curve
, find a projective
curve 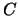 whose affine part is
whose affine part is 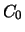 . Then find all of the points
at infinity on the projective curve
. Then find all of the points
at infinity on the projective curve 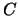 .
.
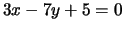
-
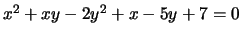
-
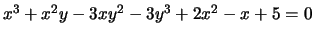
- (Jenna)
For each of the following curves
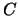 and points
and points 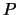 , either find
the tangent line to
, either find
the tangent line to 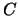 at
at 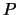 or else verify that
or else verify that 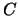 is
singular at
is
singular at 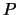 .
.
- (Alex)
Let
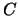 be the cubic curve
be the cubic curve
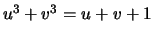 . In the
projective plane, the point
. In the
projective plane, the point 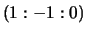 at infinity lies on this curve.
Find rational functoins
at infinity lies on this curve.
Find rational functoins 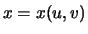 and
and 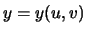 so that
so that 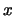 and
and 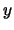 satisfy a cubic equation in Weierstrass normal form (i.e.,
satisfy a cubic equation in Weierstrass normal form (i.e.,
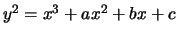 ).
).
- (Jeff)
Let
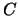 be the cubic curve in
be the cubic curve in 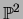 given by
Prove that the point
given by
Prove that the point 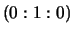 on
on 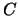 is nonsingular.
is nonsingular.
- (Jenna) Let
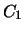 and
and 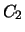 be the cubics given by the
following equations:
Find the nine points of intersection of
be the cubics given by the
following equations:
Find the nine points of intersection of 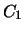 and
and 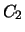 .
.
- (Jennifer) The cubic curve
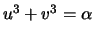 (with
(with
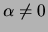 ) has a rational point
) has a rational point 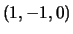 at infinity. Taking this rational point to be
at infinity. Taking this rational point to be 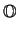 (the
identity element of the group), we can make the points
on the curve into a group.
Derive a formula for the sum
(the
identity element of the group), we can make the points
on the curve into a group.
Derive a formula for the sum 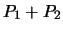 of two distinct
points
of two distinct
points
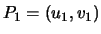 and
and
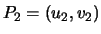 .
.
- (Mauro)
Verify that if
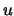 and
and 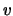 satisfy the relation
satisfy the relation
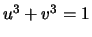 , then the quantities
, then the quantities
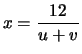
and
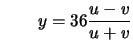
satisfy the relation
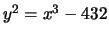 . We thus obtain a birational
transformation
. We thus obtain a birational
transformation 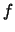 from the curve
from the curve 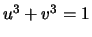 to the curve
to the curve
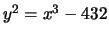 . Each of these cubic curves can have a group law defined on
it. Prove that
. Each of these cubic curves can have a group law defined on
it. Prove that 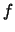 is an isomorphism of groups, where the zero
element for
is an isomorphism of groups, where the zero
element for
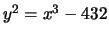 is the point
is the point 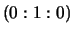 and the zero element
for
and the zero element
for 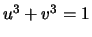 is
is 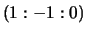 (at infinity).
(at infinity).



Next: Motivation: The Congruent Number
Up: New reading and problems
Previous: New reading and problems
William A Stein
2003-02-11
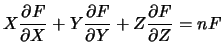
 be a curve in
be a curve in  defined by
defined by
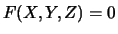 ,
where
,
where 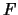 is a homogenous polynomial.
Prove that if
is a homogenous polynomial.
Prove that if
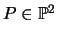 satifies the equation
satifies the equation
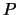 ``automatically'' satisfies
``automatically'' satisfies 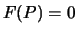 .
Thus to find the singular points on
.
Thus to find the singular points on 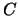 , you just
have to find the common solutions to (1);
it is not necessary to include
, you just
have to find the common solutions to (1);
it is not necessary to include 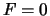 .
.
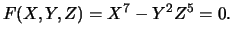
 and
and