Next: Bibliography Up: Elementary Number Theory, A Previous: Exercises Contents Index
are homomorphisms. It is injective because if
For the second part of the exercise, let
![]() and
set
and
set ![]() . Then
. Then
![]() , but
, but ![]() and
and
![]() , so
, so
![]() .
.
Thus
then we can factor
and
Since we know
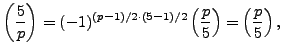
so there are two solutions if and only if
William 2007-06-01