6..
- Write down an equation
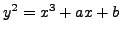 over a field
over a field
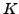 such that
such that
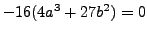 . Precisely what goes wrong
when trying to endow the set
. Precisely what goes wrong
when trying to endow the set
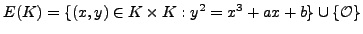 with a group structure?
with a group structure?
- One rational solution to the equation
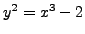 is
is 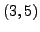 . Find a rational solution with
. Find a rational solution with 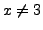 by
drawing the tangent line to
by
drawing the tangent line to 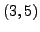 and computing the second point of
intersection.
and computing the second point of
intersection.
-
Let
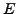 be the elliptic curve over the finite
field
be the elliptic curve over the finite
field
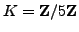 defined by the equation
defined by the equation
- List all
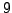 elements of
elements of 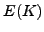 .
.
- What is the structure of
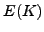 , as a product of cyclic groups?
, as a product of cyclic groups?
-
Let
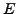 be the elliptic curve
defined by the equation
be the elliptic curve
defined by the equation
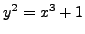 .
For each prime
.
For each prime 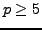 , let
, let 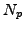 be the cardinality of the group
be the cardinality of the group
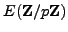 of points on this curve having coordinates
in
of points on this curve having coordinates
in
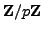 . For example, we have that
. For example, we have that
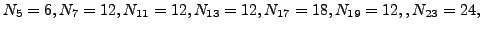 and
and 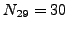 (you do not have to prove this).
(you do not have to prove this).
- For the set of primes satisfying
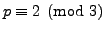 , can you see a
pattern for the values of
, can you see a
pattern for the values of 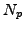 ? Make a general conjecture for the
value of
? Make a general conjecture for the
value of 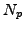 when
when
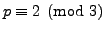 .
.
- (*) Prove your conjecture.
-
Let
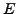 be an elliptic curve over the real numbers
be an elliptic curve over the real numbers
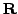 .
Prove that
.
Prove that
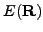 is not a finitely generated abelian group.
is not a finitely generated abelian group.
- (*)
Suppose
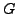 is a finitely generated abelian group.
Prove that the subgroup
is a finitely generated abelian group.
Prove that the subgroup 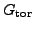 of elements of finite
order in
of elements of finite
order in 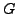 is finite.
is finite.
- Suppose
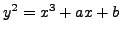 with
with
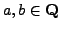 defines an elliptic
curve. Show that there is another equation
defines an elliptic
curve. Show that there is another equation
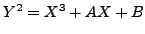 with
with
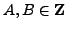 whose solutions are in bijection with the
solutions to
whose solutions are in bijection with the
solutions to
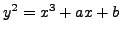 .
.
- Suppose
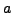 ,
, 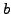 ,
, 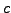 are relatively prime
integers with
are relatively prime
integers with
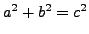 . Then there exist integers
. Then there exist integers 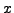 and
and 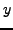 with
with 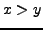 such that
such that 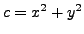 and either
and either 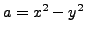 ,
, 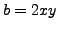 or
or
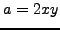 ,
, 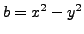 .
.
- (*) Fermat's Last Theorem for exponent
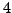 asserts
that any solution to the equation
asserts
that any solution to the equation
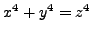 with
with
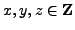 satisfies
satisfies 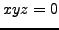 . Prove Fermat's Last
Theorem for exponent
. Prove Fermat's Last
Theorem for exponent 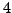 , as follows.
, as follows.
- Show that if the equation
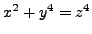 has no integer
solutions with
has no integer
solutions with 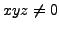 , then Fermat's Last Theorem for exponent
, then Fermat's Last Theorem for exponent 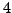 is true.
is true.
- Prove that
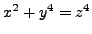 has no integer solutions with
has no integer solutions with 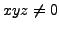 as follows.
Suppose
as follows.
Suppose
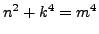 is a solution with
is a solution with 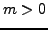 minimal amongst
all solutions. Show that there exists a solution with
minimal amongst
all solutions. Show that there exists a solution with 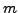 smaller
using Exercise 6.8 (consider two cases).
smaller
using Exercise 6.8 (consider two cases).
- This problem requires a computer.
- Show that the set of numbers
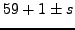 for
for 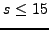 contains
contains 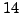 numbers that are
numbers that are 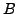 -power smooth
for
-power smooth
for 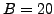 .
.
- Find the proportion of primes
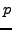 in the interval
from
in the interval
from 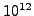 and
and
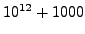 such that
such that 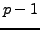 is
is
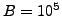 power-smooth.
power-smooth.
- (*) Prove that
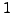 is not a congruent number by
showing that the elliptic curve
is not a congruent number by
showing that the elliptic curve 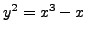 has no rational
solutions except
has no rational
solutions except 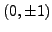 and
and 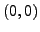 , as follows:
, as follows:
- Write
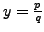 and
and
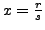 , where
, where 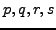 are
all positive integers and
are
all positive integers and
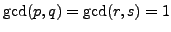 . Prove that
. Prove that 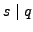 , so
, so 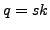 for some
for some
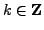 .
.
- Prove that
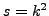 , and substitute to see that
, and substitute to see that
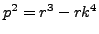 .
.
- Prove that
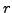 is a perfect square by supposing
that there is a prime
is a perfect square by supposing
that there is a prime 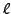 such that
such that
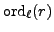 is
odd and analyzing
is
odd and analyzing
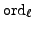 of both sides of
of both sides of
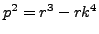 .
.
- Write
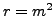 , and substitute to
see that
, and substitute to
see that
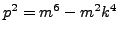 . Prove that
. Prove that 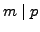 .
.
- Divide through by
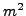 and deduce a contradiction
to Exercise 6.9.
and deduce a contradiction
to Exercise 6.9.
William
2007-06-01