Next: Finding Square Roots Up: A Proof of Quadratic Previous: A Proof of Quadratic Contents Index
Proposition 4.2.1 implies that
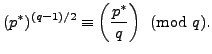
We have
But wait, what does this congruence mean, given that ![]() is not an
integer? It means that the difference
is not an
integer? It means that the difference
![]() lies in the ideal
lies in the ideal ![]() in the ring
in the ring
![]() of all polynomials in
of all polynomials in ![]() with coefficients
in
with coefficients
in
![]() .
.
The ring
![]() has characteristic
has characteristic ![]() , so
if
, so
if
![]() , then
, then
![]() .
Applying this to (4.4.3), we see that
.
Applying this to (4.4.3), we see that
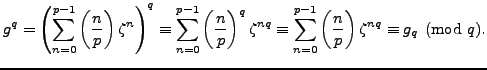
By Lemma 4.4.10,
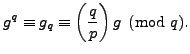
Combining this with (4.4.3) yields
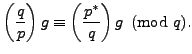
Since
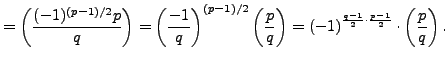 |
William 2007-06-01