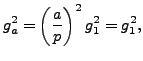A Proof of Quadratic Reciprocity Using Gauss Sums
In this section we present a beautiful proof of
Theorem 4.1.7 using algebraic identities satisfied by sums
of ``roots of unity''. The objects we introduce in the proof are of
independent interest, and provide a powerful tool to prove
higher-degree analogues of quadratic reciprocity. (For more on higher
reciprocity see [#!ireland-rosen!#]. See also Section 6 of
[#!ireland-rosen!#] on which the proof below is modeled.)
Definition 4.4 (Root of Unity)
An
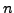
th
root of unity is a
complex number
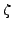
such that
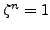
. A root of
unity
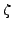
is a
primitive 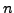
th
root of unity if
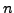
is the smallest positive integer such that
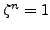
.
For example, 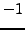 is a primitive second root of unity, and
is a primitive second root of unity, and
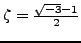 is a primitive cube root of
unity.
More generally, for any
is a primitive cube root of
unity.
More generally, for any
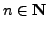 the complex number
the complex number
is a primitive 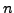 th root of unity (this follows from the identity
th root of unity (this follows from the identity
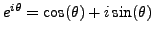 ). For the rest of this
section, we fix an odd prime
). For the rest of this
section, we fix an odd prime 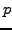 and the primitive
and the primitive 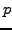 th
root
th
root
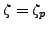 of unity.
of unity.
SAGE Example 4.4
In SAGE use the CyclotomicField command to create an exact
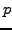
th root of
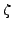
unity. Expressions in
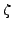
are always
re-expressed as polynomials in
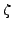
of degree at most
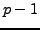
.
sage: K.<zeta> = CyclotomicField(5)
sage: zeta^5
1
sage: 1/zeta
-zeta^3 - zeta^2 - zeta - 1
Definition 4.4 (Gauss Sum)
Fix an odd prime
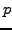
. The
Gauss sum associated to an integer
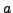
is
where
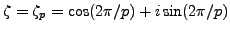
.
Note that 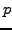 is implicit in the definition of
is implicit in the definition of 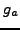 . If we were to
change
. If we were to
change 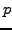 , then the Gauss sum
, then the Gauss sum 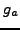 associated to
associated to 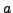 would be
different. The definition of
would be
different. The definition of 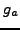 also depends on our choice
of
also depends on our choice
of 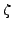 ; we've chosen
; we've chosen
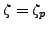 , but could have chosen
a different
, but could have chosen
a different 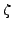 and then
and then 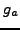 could be different.
could be different.
SAGE Example 4.4
We define in SAGE a function gauss_sum and compute
the Gauss sum
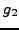
for
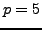
:
sage: def gauss_sum(a,p):
... K.<zeta> = CyclotomicField(p)
... return sum(legendre_symbol(n,p) * zeta^(a*n) for n in range(p))
sage: g2 = gauss_sum(2,5); g2
2*zeta^3 + 2*zeta^2 + 1
sage: g2.complex_embedding()
-2.23606797749979 + 0.000000000000000333066907387547*I
sage: g2^2
5
Here
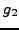
is initially output as a polynomial in
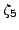
,
so there is no loss of precision. The complex_embedding
command shows some embedding of
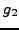
into the complex numbers,
which is only correct to about the first 15 digits. Note
that
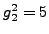
, so
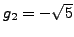
.
Figure 4.1:
Gauss sum 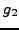 for
for 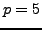
![\includegraphics[width=\textwidth]{graphics/gauss_sum.eps}](img1383.png) |
Figure 4.1 illustrates the Gauss sum 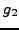 for
for 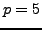 .
The Gauss sum is obtained by adding the points on the unit circle,
with signs as indicated, to obtain the real number
.
The Gauss sum is obtained by adding the points on the unit circle,
with signs as indicated, to obtain the real number 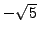 . This
suggests the following proposition, whose proof will require some
work.
. This
suggests the following proposition, whose proof will require some
work.
SAGE Example 4.4
We illustrate using SAGE that the proposition is
correct for
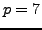
and
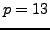
:
sage: [gauss_sum(a, 7)^2 for a in range(1,7)]
[-7, -7, -7, -7, -7, -7]
sage: [gauss_sum(a, 13)^2 for a in range(1,13)]
[13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13, 13]
In order to prove the proposition, we introduce a few lemmas.
Proof.
If
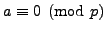
, then
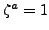
, so the sum equals the number of summands,
which is
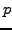
. If
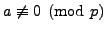
, then we use then
identity
with
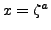
. We have
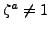
, so
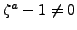
and

Lemma 4.4
If 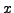 and
and 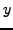 are arbitrary integers, then
are arbitrary integers, then
Proof.
This follows from Lemma
4.4.7 by
setting
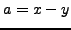
.

Proof.
By definition
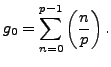 |
(4.4.1) |
By Lemma
4.1.4, the map
is a surjective homomorphism of groups. Thus half the
elements of
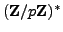
map to
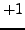
and half map to
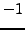
(the
subgroup that maps to
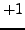
has index
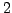
). Since
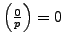
, the
sum (
4.4.1) is
0
.

Proof.
When
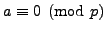
the lemma follows from
Lemma
4.4.9, so suppose that
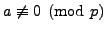
. Then
Here we use that multiplication by
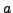
is
an automorphism of
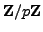
. Finally, multiply both sides by
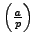
and use that
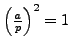
.

We have enough lemmas to
prove Proposition 4.4.5.
Proof.
[Proof of Proposition
4.4.5]
We evaluate the sum
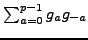
in two different ways. By
Lemma
4.4.10, since
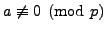
we have
where the last step follows from Proposition
4.2.1
and that
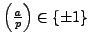
. Thus
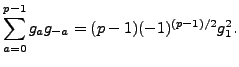 |
(4.4.2) |
On the other hand, by definition
Let
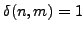
if
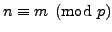
and
0
otherwise.
By Lemma
4.4.8,
Equate (
4.4.2) and the above equality,
then cancel
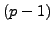
to see that
Since
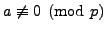
, we have
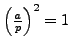
, so by Lemma
4.4.10,
and the proposition is proved.

Subsections
William
2007-06-01
![]() for
for ![]() .
The Gauss sum is obtained by adding the points on the unit circle,
with signs as indicated, to obtain the real number
.
The Gauss sum is obtained by adding the points on the unit circle,
with signs as indicated, to obtain the real number ![]() . This
suggests the following proposition, whose proof will require some
work.
. This
suggests the following proposition, whose proof will require some
work.
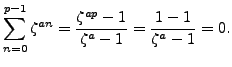
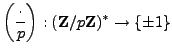
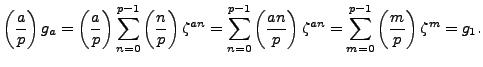
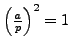 .
.
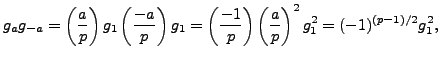
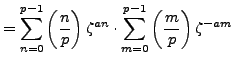
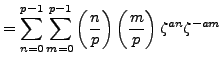
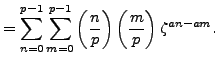
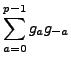
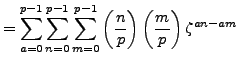
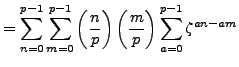
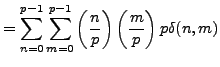
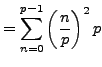
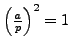 , so by Lemma 4.4.10,
, so by Lemma 4.4.10,