Next: The Shafarevich-Tate Group Up: Galois Cohomology Previous: The inf-res Sequence Contents Index
For any ![]() -module
-module ![]() and any
and any ![]() , let
, let
Let ![]() denote a separable closure of
denote a separable closure of ![]() and
suppose
and
suppose ![]() is a (continuous)
is a (continuous)
![]() -module.
(Note - if
-module.
(Note - if ![]() has characteristic
has characteristic ![]() , then a separable
closure is the same thing as an algebraic closure.)
For any subfield
, then a separable
closure is the same thing as an algebraic closure.)
For any subfield
![]() that contains
that contains ![]() ,
let
,
let ![]() .
Let
.
Let
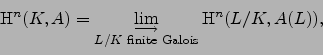
One can prove (see [Cp86, Ch. V]) that changing the
choice of separable closure ![]() only changes
only changes ![]() by
unique isomorphism, i.e., the construction is essentially independent
of the choice of seperable closure.
by
unique isomorphism, i.e., the construction is essentially independent
of the choice of seperable closure.
William 2007-05-25