Computing
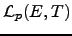
Fix notation as in Section 1.5. In particular,  is an elliptic curve over
is an elliptic curve over 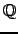 ,
, 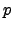 is an odd prime of good ordinary
reduction for
is an odd prime of good ordinary
reduction for  , and
, and 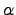 is the root of
is the root of 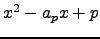 with
with
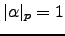 .
.
For each integer 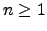 , define a polynomial
, define a polynomial
Recall that
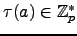 is the Teichmuller lift of
is the Teichmuller lift of 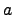 .
.
Proposition 1.20
We have that the 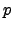 -adic limit of these polynomials is the
-adic limit of these polynomials is the 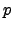 -adic
-adic
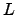 -series:
-series:
This convergence is coefficient-by-coefficient, in the sense that
if
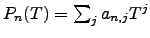 and
and
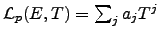 , then
, then
We now give a proof of this convergence and in doing so obtain an
upper bound for
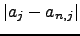 .
.
For any choice 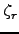 of
of 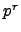 -th root
of unity in
-th root
of unity in 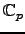 ,
let
,
let 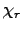 be the
be the 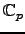 -valued
character of
-valued
character of
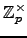 of order
of order 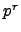 which
factors through
which
factors through
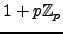 and sends
and sends 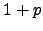 to
to 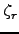 .
Note that the conductor of
.
Note that the conductor of 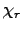 is
is 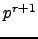 .
.
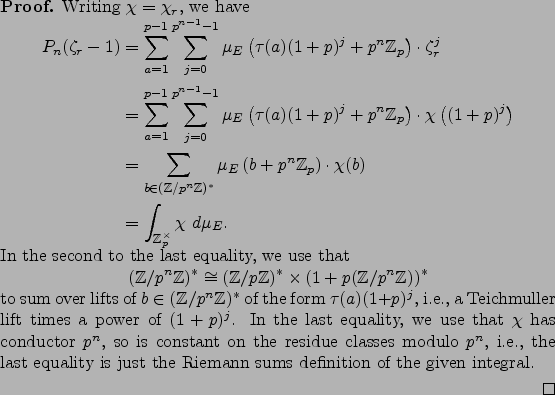
For each positive integer 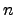 , let
, let
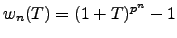 .
.
Corollary 1.22
We have that


As above, let 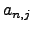 be the
be the 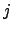 th coefficient of
the polynomial
th coefficient of
the polynomial 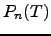 .
Let
.
Let
so that
![$p^{c_n} P_{n}(T) \in \mathbb{Z}_p[T]$](img253.png) , i.e.,
, i.e., 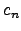 is the smallest power of
is the smallest power of 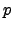 that clears the denominator.
Note that
that clears the denominator.
Note that 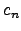 is an integer since
is an integer since
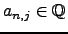 .
Probably if
.
Probably if ![$E[p]$](img256.png) is irreducible then
is irreducible then 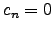 - see
Question 1.13.
Also, for any
- see
Question 1.13.
Also, for any 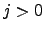 ,
let
,
let
be the min of the valuations of the coefficients of 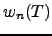 ,
as in Lemma 1.23.
,
as in Lemma 1.23.
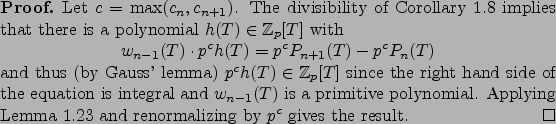
For 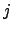 fixed,
fixed,
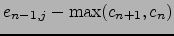 goes to infinity as
goes to infinity as 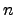 grows since the
grows since the 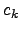 are uniformly
bounded (they are bounded by the power of
are uniformly
bounded (they are bounded by the power of 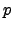 that
divides the order of the cuspidal subgroup of
that
divides the order of the cuspidal subgroup of  ).
Thus,
).
Thus, 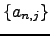 is a
Cauchy and Proposition 1.24 implies that that
is a
Cauchy and Proposition 1.24 implies that that
Remark 1.25
Recall that presently there is not a single
example where we can provably show that
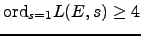
. Amazingly
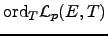
is ``computable in practice'' because Kato has proved,
using his Euler system in
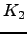
, that
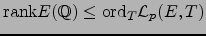
by proving a divisibility
predicted by Iwasawa Theory. Thus computing elements of
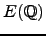
gives
a provable lower bound, and approximating
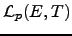
using Riemann
sums gives a provable upper bound - in practice these meet.
William
2007-05-25
![]() , define a polynomial
, define a polynomial
![\begin{displaymath}
P_{n}(T) =
\sum_{a=1}^{p-1} \left( \sum_{j=0}^{p^{n-1}-1} ...
...\mathbb{Z}_p\right) \cdot (1+T)^j \right) \in \mathbb{Q}_p[T].
\end{displaymath}](img220.png)
![]() and
and
![]() , then
, then
![]() of
of ![]() -th root
of unity in
-th root
of unity in ![]() ,
let
,
let ![]() be the
be the ![]() -valued
character of
-valued
character of
![]() of order
of order ![]() which
factors through
which
factors through
![]() and sends
and sends ![]() to
to ![]() .
Note that the conductor of
.
Note that the conductor of ![]() is
is ![]() .
.
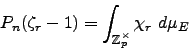
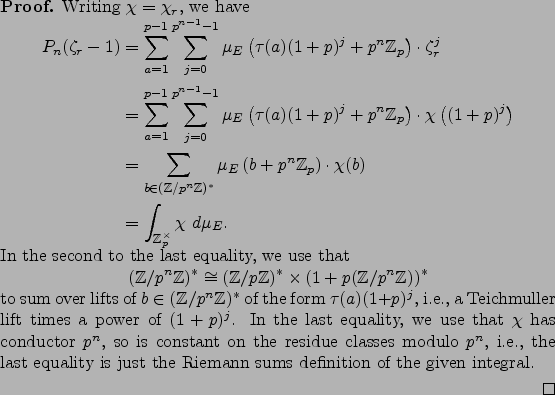
![]() , let
, let
![]() .
.


![]() be the
be the ![]() th coefficient of
the polynomial
th coefficient of
the polynomial ![]() .
Let
.
Let
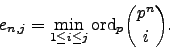
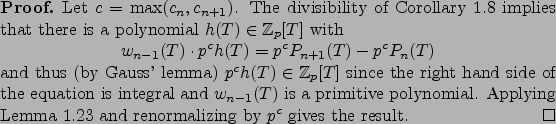
![]() fixed,
fixed,
![]() goes to infinity as
goes to infinity as ![]() grows since the
grows since the ![]() are uniformly
bounded (they are bounded by the power of
are uniformly
bounded (they are bounded by the power of ![]() that
divides the order of the cuspidal subgroup of
that
divides the order of the cuspidal subgroup of ![]() ).
Thus,
).
Thus, ![]() is a
Cauchy and Proposition 1.24 implies that that
is a
Cauchy and Proposition 1.24 implies that that