Proof.
The proof is similar to the proof of Euclid's Theorem, but, for variety,
I will explain it in a slightly different way.
Suppose
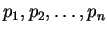 are primes of the form
are primes of the form 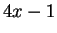 . Consider
the number
. Consider
the number
Then
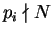
for any
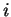
. Moreover, not every prime
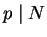
is
of the form
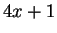
; if they all were, then
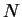
would also be of the
form
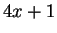
, which it is not.
Thus there is a
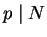
that is of the form
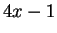
. Since
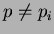
for any
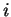
, we have found another prime of the form
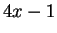
. We can repeat
this process indefinitely, so the set of primes of the form
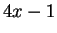
is infinite.

Example 2.2
Set
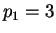
,
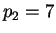
. Then
is a prime of the form
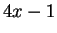
.
Next
which is a again a prime of the form
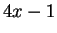
.
Again:
This time
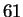
is a prime, but it is of the form
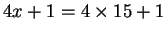
.
However,
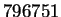
is prime and
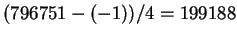
.
We are unstoppable
This time the small prime,
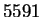
, is of the form
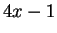
and the large
one is of the form
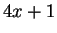
.
Etc!
![]() are primes of the form
are primes of the form ![]() . Consider
the number
. Consider
the number