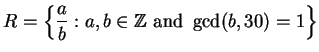
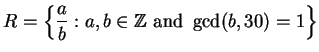
If we were to try a similar proof in ![]() , we run into trouble.
We would let
, we run into trouble.
We would let
![]() , which is a unit,
hence not a nontrivial product of primes.
, which is a unit,
hence not a nontrivial product of primes.
Joke (Lenstra). ``There are infinitely many composite
numbers. Proof: Multiply together the first ![]() primes and don't add
primes and don't add ![]() .''
.''
According to
http://www.utm.edu/research/primes/largest.html
the largest known prime is